2003年青岛市中等学校招生考试
数学试题
第一卷
一、选择题(本题共有8道小题,每小题3分,满分24分)每小题的四个结论中只有一个是正确的).
1. 方程 =0 的根的情况是( ).
=0 的根的情况是( ).
(A)有两个相等的实数根 (B)有两个不相等的实数根
(C)两个实数根的和与积都等于1 (D)无实数根
2. 有三个点A、B、C,过其中每两个点画直线,可以画出( )条直线.
(A)1 (B)3 (C)1或3 (D)无法确定
3. 函数 中自变量x的取值范围是(
).
中自变量x的取值范围是(
).
(A)x≥5(B) x>5(C)x≥-5 (D)x≤5
4. 在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆,必与( ).
(A)x轴相交 (B)y轴相交 (C)x轴相切 (D)y轴相切
5. 若菱形的边长为1cm,其中一内角为60°,则它的面积为( ).
(A) 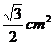 (B)
(B) 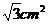 (C)
(C) 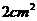 (D)
(D) 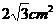
6. 一列火车从青岛站出发,加速行驶一段时间后开始匀速行驶.过了一段时间,火车到达下一个车站.乘客上下车后,火车又加速,一段时间后再次开始匀速行驶.下面( )图可以近似地刻画出火车在这段时间内的速度变化情况.
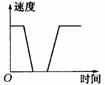
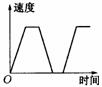
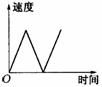

(A)(B)(C)(D)
7. “圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,间径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为 ( )
(A) 12.5寸 (B)13寸
(C) 25寸 (D)26寸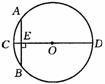
8. 已知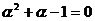 ,
,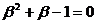 ,且α≠β,则
,且α≠β,则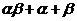 的值为( ).
的值为( ).
(A)2 (B)一2 (C)一1 (D)0
第二卷
二、填空题(本题共有8道小题,每小题3分,满分24分)
9. 九年义务教育三年制初级中学教科书《代数》第三册第52页的例2是这样的:“解方程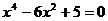 ”.这是一个一元四次方程,根据该方程的特点,它的解法通常是:设
”.这是一个一元四次方程,根据该方程的特点,它的解法通常是:设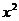 =y,那么
=y,那么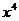 =
=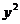 ,于是原方程可变为
,于是原方程可变为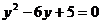 ……①,解这个方程得:y1=1,y2=5.当y=1时,
……①,解这个方程得:y1=1,y2=5.当y=1时,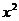 =1,∴ x=土1;当 y=5时,
=1,∴ x=土1;当 y=5时,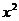 =5,∴ x=土
=5,∴ x=土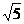 。所以原方程有四个根:x1=1,x2=-1,x3=
。所以原方程有四个根:x1=1,x2=-1,x3=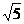 ,x4=-
,x4=-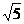 。
。
⑴ 在由原方程得到方程①的过程中,利用 法达到降次的目的,体现了转化的数学思想.
⑵ 解方程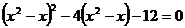 时,若设y=
时,若设y=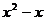 ,则原方程可化为
.
,则原方程可化为
.
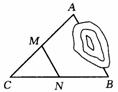
10. 如图,A、B两点被池塘隔开,在 AB外选一点 C,连结 AC和 BC,并分别找出它们的中点 M、N.若测得MN=15m,则A、B两点的距离为 .
11. 当a<l且a≠0时,化简 =
.
=
.
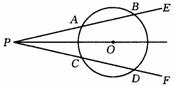
12. 如图,点O是∠EPF的平分线上一点,⊙O和∠EPF的两边分别交于点A、B和C、D,根据上述条件,可以推出 .(要求:填写一个你认为正确的结论即可,不再标注其他字母,不写推理过程)
13. 某林业部门为对辖区内面积为1200公顷的山林进行林业资源调查,工作人员在山林中挑选了一块面积为1亩的样本地,经实地清点,该样本地的树木数量为196棵,估计该山林的树木总量约为 棵(用科学记数法表示;1公顷=15亩).
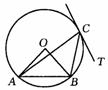
14. 如图,△ABC内接于圆⊙O,CT切⊙O于C,∠ABC=100°,∠BCT=40°,则∠AOB= .
15. 我市一科技园区2002年全年高新技术产品出口额达到35亿美元,而2003年l-6月份,该科技园区的高新技术产品出口额达18亿美元,比去年同期增长了20%,按这个增长势头,预计2003年7-12月份的出日额将比去年同期增长25%,那么该科技园区2003年全年的高新技术产品出口额预计为 亿美元。
16. 探究数字“黑洞”:“黑洞”原指非常奇怪的天体,它体积小,密度大,吸引力强,任何物体到了它那里都别想再“爬”出来.无独有偶,数字中也有类似的“黑洞”,满足某种条件的所有数,通过一种运算,都能被它“吸”进去,无一能逃脱它的魔掌.譬如:任意找一个3的倍数的数,先把这个数的每一个数位上的数字都立方,再相加,得到一个新数,然后把这个新数的每一个数位上的数字再立方、求和,…,重复运算下去,就能得到一个固定的数T=
,我们称它为数字“黑洞”.
T为何具有如此魔力?通过认真的观察、分析,你一定能发现它的奥秘!
三、作图题(本题满分 4分)用圆规、直尺作图,不写作法,但要保留作图痕迹.
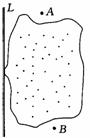
17. 某汽车探险队要从A城穿越沙漠去B城,途中需要到河流L边为汽车加水,汽车在河边哪一点加水,才能使行驶的总路程最短?请你在图上画出这一点.
四、解答题(本题共有 9道小题,满分 68分)
18. (6分)解方程组: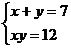
19. (6分)在世界环境日到来之际,希望中学开展了“环境与人类生存”主题研讨活动,活动之一是对我们的生存环境进行社会调查,并对学生的调查报告进行评比.初三?3班将本班50篇学生调查报告得分进行整理(成绩均为整数),列出了频率分布表,并画出了频率分布直方图(部分)如下:
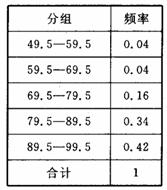

根据以上信息回答下列问题:
⑴ 该班90分以上(含90分)的调查报告共有
篇。
⑵ 该班被评为优秀等级(80分及80分以上)的调查报告占
%;
⑶ 补全频率分布直方图.
20.(6分)人民海关缉私巡逻艇在东海海域执行巡逻任务时,发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只,正以24海里/小时的速度向正东方向航行.为迅速实施检查,巡逻艇调整好航向,以26海里/小时的速度追赶,在涉嫌船只不改变航向和航速的前提下,问⑴需要几小时才能追上?(点B为追上时的位置)⑵确定巡逻艇的追赶方向(精确到0.1°).
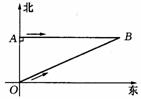
参考数据:
sin66.8°≈ 0.9191 cos
66.8°≈ 0.393
sin67.4°≈ 0.9231 cos
67.4°≈ 0.3846
sin68.4°≈ 0.9298 cos
68.4°≈ 0.368l
sin70.6°≈ 0.9432 cos70.6°≈ 0.3322
21. (6分)在争创全国卫生城市的活动中,我市一“青年突击队”决定义务清运一堆重达100吨的垃圾.开工后,附近居民主动参加到义务劳动中,使清运垃圾的速度比原计划提高了一倍,结果提前4小时完成任务,问“青年突击队”原计划每小时清运多少吨垃圾?
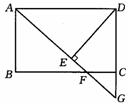
22. (8分)如图,在矩形 ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.根据上述条件,请在图中找出一对全等三角形,并证明你的结论.
23. (8分)某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.中商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,什么情况下到甲商场购买更优惠?
24.(8分)在抗击“非典”的斗争中,某市根据疫情的发展状况,决定全市中、小学放假两周,以切实保障广大中、小学生的安全.腾飞中学初三(1)班的全体同学在自主完成学习任务的同时,不忘关心同学们的安危,两周内全班每两个同学都通过一次电话,互相勉励,共同提高.如果该班有56名同学,那么同学们之间共通了多少次电话?
为解决该问题,我们可把该班人数n与通电话次数s间的关系用下列模型来表示:
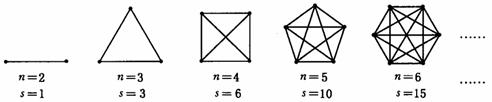
⑴ 若把n作为点的横坐标,s作为纵坐标,根据上述模型中的数据,在给出的平面直角坐标系中,描出相应各点,并用平滑的曲线连接起来;
⑵ 根据日中各点的排列规律,猜一猜上述各点会不会在某一函数的图像上?如果在,求出该函数的解析式;
⑶根据⑵中得出的函数关系式,求该班56名同学间共通了多少次电话.
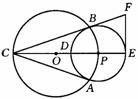
25. (10分)已知:如图,⊙O与⊙P相交于A、B两点,点 P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,过点 E作EF⊥CE交CB的延长线于F.
⑴ 求证:BC是⊙P的切线;
⑵ 若CD=2,CB=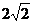 ,求EF的长;
,求EF的长;
⑶ 若设k=PE:CE,是否存在实数k,使△PBD恰好是等边三角形?若存在,求出k的值;若不存在,请说明理由.
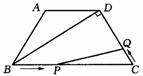
26. (10分)已知:如图,梯形ABCD中,AD∥BC,AB=CD=3cm,∠C=60°,BD⊥CD.
⑴ 求BC、
AD的长度;
⑵ 若点P从点B开始沿BC边向点C以2cm/秒的速度运动,点Q从点C开始沿CD边向点D以1cm/秒的速度运动,当 P、Q分别从B、C同时出发时,写出五边形ABPQD的面积S与运动时间t之间的函数关系式,并写出自变量t的取值范围(不包含点P在B、C两点的情况);
⑶ 在⑵的前提下,是否存在某一时刻t,使线段PQ把梯形ABCD分成两部分的面积比为1∶5?若存在,求出t的值;若不存在,请说明理由.