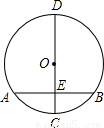
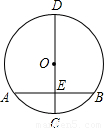
摘要： “圆材埋壁 是我国古代著名数学著作中的问题:“今有圆材.埋在壁中.不知大小以锯锯之.深一寸.锯道长一尺.间径几何? 用数学语言可表述为:“如图.CD为⊙O的直径.弦AB⊥CD于E.CE＝1寸.AB＝10寸.则直径CD的长为 ( ) (A) 12．5寸 (B)13寸 (C) 25寸 (D)26寸
网址：http://m.1010jiajiao.com/timu_id_656553[举报]
“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”此问题的实质就是解决下面的问题：“如图，CD为⊙O的直径，弦AB⊥CD于点E，CE=1，AB=10，求CD的长”．根据题意可得CD的长为“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺，间径几何？”用数学语言可表述为：“如图，CD为⊙O的直径，弦AB⊥CD于E，CE=1寸，AB=10寸，求直径CD的长．”
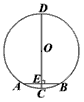
“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”此问题的实质就是解决下面的问题：“如图，CD为⊙O的直径，弦AB⊥CD于点E，CE=1，AB=10，求CD的长”．根据题意可得CD的长为 ．
查看习题详情和答案>>
查看习题详情和答案>>
