1.如图，有一块矩形纸片ABCD，AB＝8，AD＝6.　将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则△CEF的面积为（　　　）

　A.2　　　B.4　　　C.6　　　D.8

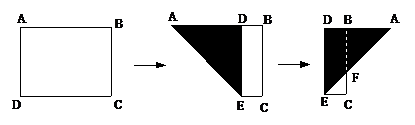
2.若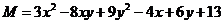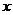（，是实数），则M的值一定是（　　　）

　A.正数　　　B.负数　　　C.零　　　D.整数

3.已知点I是锐角三角形ABC的内心，A₁，B₁，C₁分别是点I关于边BC，CA，AB的对称点.　若点B在△A₁ B₁ C₁的外接圆上，则∠ABC等于（　　　）

　A.30°　　　B.45°　　　C.60°　　　D.90°

4.设，则与A最接近的正整数是（　　　）

　A.18　　　B.20　　　C.24　　　D.25

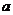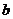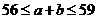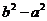5.设，是正整数，且满足，，则等于（　　　）

　A.171　　　B.177　　　C.180　　　D.182

6.在一个圆形时钟的表面，OA表示秒针，OB表示分针（O为两针的旋转中心）.　若现在时间恰好是12点整，则经过＿＿＿＿秒钟后，△OAB的面积第一次达到最大.

7.在直角坐标系中，抛物线（m＞0）与x轴交于A，B两点.　若A，B两点到原点的距离分别为OA，OB，且满足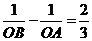，则m的值等于＿＿＿＿.

8.有两副扑克牌，每副牌的排列顺序是：第一张是大王，第二张是小王，然后是黑桃、红桃、方块、梅花四种花色排列，每种花色的牌又按A，2，3，…，J，Q，K的顺序排列.　某人把按上述排列的两副扑克牌上下叠在一起，然后从上到下把第一张丢掉，把第二张放在最底层，再把第三张丢掉，把第四张放在最底层，……如此下去，直至最后只剩下一张牌，则所剩的这张牌是＿＿＿＿＿.

9.已知D，E分别是△ABC的边BC，CA上的点，且BD＝4，DC＝1，AE＝5，EC＝2.　连结AD和BE，它们相交于点P.　过点P分别作PQ∥CA，PR∥CB，它们分别与边AB交于点Q，R，则△PQR的面积与△ABC的的面积之比为＿＿＿＿.

10.已知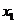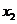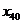，，…，都是正整数，且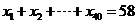.　若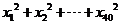的最大值为A，最小值为B，则A＋B的值等于＿＿＿＿.

11.8个人乘速度相同的两辆小汽车同时赶往火车站，每辆车乘4人（不包括司机）.　其中一辆小汽车在距离火车站10km的地方出现故障，此时距停止检票的时间还有28分钟.　这时惟一可利用的交通工具是另一辆小汽车，已知包括司机在内这辆车限乘5人，且这辆车的平均速度是60km/h，人步行的平均速度是5km/h..　试设计一种方案，通过计算说明这8个人能够在停止检票前赶到火车站.

12.如图，半径不等的两圆相交于A，B两点，线段CD经过点A，且分别交两圆于C，D两点.　连结BC，BD，设P，Q，K分别是BC，BD，CD的中点，M，N分别是弧BC和弧BD的中点.　求证：

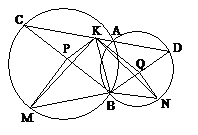　（1）；

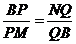　（2）△KPM∽△NQK

13.已知p，q都是质数，且使得关于x的二次方程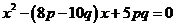至少有一个正整数根，求所有的质数对（p，q）.

14.从1，2，…，205共205个正整数中，最多能取出多少个数，使得对于取出来的数中的任意三个数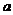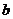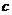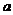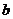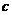，，（＜＜＝，都有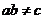.