2006――2007学年度第一学期
海口市八年级数学科期终检测题
时间:100分钟 满分:100分 得分:
一、选择题(每小题2分,共20分)
1.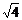 的平方根是
的平方根是
A.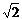 B.±
B.±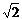 C.2 D.±2
C.2 D.±2
2.下列计算错误的是
A.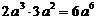 B.
B.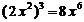
C.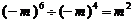 D.
D.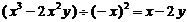
3.若直角三角形有两条边的长分别为3和4,则另一条边的长为
A.5 B.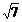 C.5或
C.5或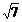 D.不能确定
D.不能确定
4.A为数轴上表示-1的点,将点A沿数轴向右平移3个单位到点B,则点B表示的实数为
A.3 B.
5. 下列各图中,是中心对称图形的是
 |
6.下列说法正确的是
A.等边三角形既是轴对称图形,又是中心对称图形
B.等边三角形既是旋转对称图形,又是中心对称图形
C.等边三角形既是旋转对称图形,又是轴对称图形
D.等边三角形是轴对称图形,但不是旋转对称图形
7. 如图1,四边形ABCD为平行四边形,延长BA,下列各式不一定成立的是
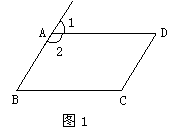 A.∠1+∠2=180° B.∠2+∠B=180°
A.∠1+∠2=180° B.∠2+∠B=180°
C.∠B+∠C=180° D.∠2+∠C=180°
8.下面的性质中矩形具有而菱形不一定具有的是
A.对角线互相平分 B.对角线互垂直
C.对角线相等 D.对角线平分一组对角
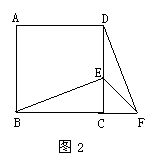
9. 如图2,正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针旋转90°得到△DCF,若∠BEC=60°,则∠EFD的度数为
A.25° B.20° C.15° D.10°
 |
|||
 |
|||
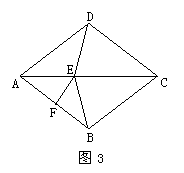
10.如图3,在菱形ABCD中,AB的垂直平分线交对角线AC于E,F为垂足,连结DE、BE,则图中与∠BAC相等的角有
A.5个 B.6个 C.7个 D.8个
二、填空题(每小题3分,共24分)
11.任意写出3个无理数,其中1个带根号,另外2个不带根号: ,
, .
12.计算: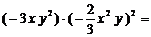 .
.
13.将一个等腰直角三角形绕着它的直角顶点旋转 次,每次旋转 度可得到一个正方形.
14.若一个正方形的对角线长为4,则它的边长为 .
15.如图4,已知:在 ABCD中, AC、BD相交于点O,AC=10,BD=8,CD=6,则△OAB的周长为
.
ABCD中, AC、BD相交于点O,AC=10,BD=8,CD=6,则△OAB的周长为
.
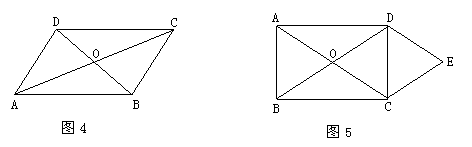 |
16. 如图5,矩形ABCD的对角线相交于O,把△ABO平移到△DCE的位置,则四边形OCED的形状是 .
 17.已知菱形的边长为5cm,一条对角线长8cm,这
17.已知菱形的边长为5cm,一条对角线长8cm,这
个菱形的面积为 cm2.
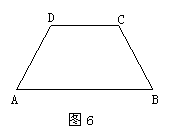
18.如图6,在梯形ABCD中,AB∥DC,AD=DC=CB=1,
AB=2,则∠A的度数等于 .
三、解答题(共56分)
19. (4分)用大小完全相同的200块正方形地板砖正好铺满一间面积为72m2的客厅,求这样的一块正方形地板砖的边长是多少.
20.先化简,再求值(每小题5分,共10分)
(1) 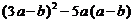 ,其中
,其中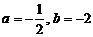 .
.
(2) 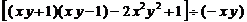 , 其中
, 其中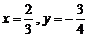 .
.
21.把下列多项式分解因式(每小题5分,共10分)
(1)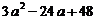 (2)
(2)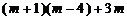
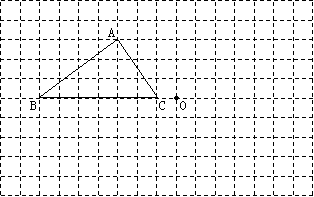
22. (6分) 在下面的方格纸中,先画△A1B1C1,使△A1B1C1与△ABC关于点O中心对称,再画出将△A1B1C1向上平移3格后的△A2B2C2.
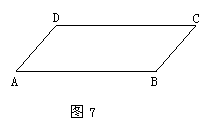
23.(7分)如图7,已知 ABCD的周长为24,且AB=2AD,求
ABCD的周长为24,且AB=2AD,求 ABCD四条边的长.
ABCD四条边的长.
 |
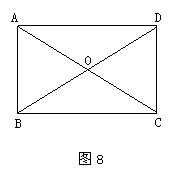
24. (7分)如图8,矩形ABCD的两条对角线交于点O,且AC=2AB,你能说明△0AB是等边三角形吗?请写出理由.
 |
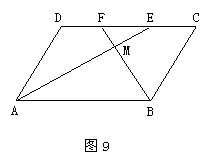
25. (12分)如图9,在 ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并说明理由.
 |
2006―2007学年度第一学期
一、BACBB CDCCA
二、11.答案不唯一,如: ,π,0.1010010001… 12.
,π,0.1010010001… 12. 
13.3,90 14. 2 15.15 16.菱形 17.24 18. 60°
15.15 16.菱形 17.24 18. 60°
三、19. (m)
(m)
20.(1)原式= …………………………………………
2分
…………………………………………
2分
= ………………………………………… 3分
………………………………………… 3分
当 时,
时,
原式= ………………………………… 4分
………………………………… 4分
=1-1+4
=4. ………………………………………… 5分
(2)原式= …………………………………… 1分
…………………………………… 1分
= ………………………………………… 2分
………………………………………… 2分
= ………………………………………… 3分
………………………………………… 3分
当 时,
时,
原式= ………………………………………… 4分
………………………………………… 4分
= .
………………………………………… 5分
.
………………………………………… 5分
21.(1)原式=3(a2-8a+16) ………………………………………… 2分
=3(a-4)2. ………………………………………… 5分
(2)原式=m2+m-4m-4+3m ………………………………………… 2分
=m2-4 ………………………………………… 3分
=(m+2)(m-2). ………………………………………… 5分
22. 正确画△A1B1C1给3分,正确画△A2B2C2给3分,共6分.
23. 在 ABCD中,AB=DC,AD=BC.
………………………………………… 2分
ABCD中,AB=DC,AD=BC.
………………………………………… 2分
∴ AB+AD= .
………………………………………… 3分
.
………………………………………… 3分
∵ AD=2AD,
∴ 2AD+AD=12. ………………………………………… 4分
∴ AD=4,BC=4. ………………………………………… 6分
AB=DC=8. ………………………………………… 7分
24. △OAB是等边三角形的理如下:
在矩形ABCD中,OA=0C,OB=OD, ………………………………………… 2分
AC=BD, ………………………………………… 4分
∴ OA= AC,OB=
AC,OB= BD.
………………………………………… 6分
BD.
………………………………………… 6分
又∵ AB= AC,
AC,
∴ OA=OB=AB.
即△OAB是等边三角形. ………………………………………… 7分
25. (1)在 ABCD中,∠DAB+∠ABC=180°,………………………………………… 2分
ABCD中,∠DAB+∠ABC=180°,………………………………………… 2分
∵ AE,BF分别平分∠DAB和∠ABC,
∴ ∠EAB+∠FBA=90°, ………………………………………… 3分
∴ AE⊥BF. ………………………………………… 4分
(2)在 ABCD中,DA=CB,DC∥AB, ………………………………………… 6分
ABCD中,DA=CB,DC∥AB, ………………………………………… 6分
∴ ∠EAB=∠DEA, ………………………………………… 7分
∵ ∠DAE=∠EAB,
∴ ∠DAE=∠DEA, ………………………………………… 8分
∴DA=DE. ………………………………………… 9分
同理,得 CF=CB. ………………………………………… 10分
∴ DE=CF, ………………………………………… 11分
∴ DE-FE=CF-FE,
即 DF=CF. ………………………………………… 12分