2006学年浙江省五校联考(一)
数学(文科)试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.卷面共150分,考试时间120分钟.
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、已知集合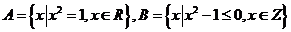 ,则有( )
,则有( )
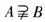
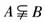 (A)
(A)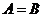 (B) (C) (D)A=CRB
(B) (C) (D)A=CRB
2、具有A、B、C三种性质的总体,其容量为63,将A、B、C三种性质的个体按1∶2∶4的比例进行分层抽样调查,如果抽取的样本容量为21,则A、B、C三种元素分别抽取( )
(A)12、6、3 (B)12、3、6 (C)3、6、12 (D)3、12、6
3、下列函数中最小正周期为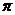 的是( )
的是( )
(A)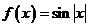 (B)
(B)
(C)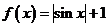 (D)
(D)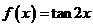
4、已知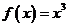 ,则实数
,则实数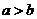 是
是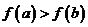 的( )条件
的( )条件
(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要
5、函数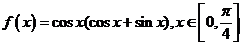 的值域是( )
的值域是( )
(A)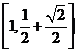 (B)
(B)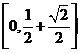 (C)
(C)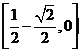 (D)
(D)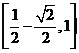
6、已知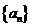 是正项的等差数列,如果满足:
是正项的等差数列,如果满足: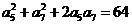 ,则数列
,则数列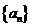 的前11项的和为( )
的前11项的和为( )
(A)8 (B)44 (C)56 (D)64
7、函数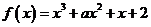 在
在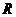 上存在极值点,则实数
上存在极值点,则实数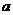 的取值范围是( )
的取值范围是( )
(A)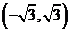 (B)
(B)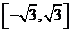
(C)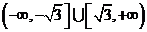 (D)
(D)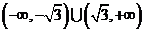
8、同时抛掷三枚骰子,出现正面朝上的点数之和不大于5的概率是( )
(A)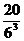 (B)
(B)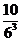 (C)
(C)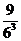 (D)
(D)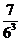
9、已知平面向量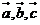 满足
满足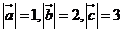 ,且向量
,且向量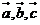 两两所成的角相等,则
两两所成的角相等,则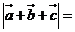 ( )
( )
(A) (B)
(B)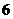 或
或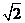 (C)6
(D)
(C)6
(D) 或
或
10、设二次函数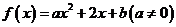 ,若方程
,若方程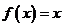 无实数根,则方程
无实数根,则方程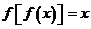 的实数根的个数为( )
的实数根的个数为( )
(A)0 (B)2 (C)4 (D)4个以上
第Ⅱ卷(非选择题,共100分)
二、填空题:本大题共4小题,每小题4分,共16分.
11、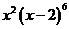 展开式中
展开式中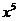 的系数是 ▲ .
的系数是 ▲ .
12、若关于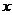 的不等式
的不等式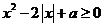 恒成立,则实数
恒成立,则实数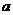 的取值范围是 ▲ .
的取值范围是 ▲ .
13、用0,1,2,3,4这五个数字组成无重复数字的五位数,其中恰有一个偶数夹在两个奇数之间的五位数的个数是 ▲ (用数字作答).
14、在直角三角形ABC中,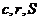 分别表示它的斜边、内切圆半径和面积,则
分别表示它的斜边、内切圆半径和面积,则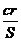 的最小值是 ▲
.
的最小值是 ▲
.
三、解答题:本大题共6小题,每小题14分,共84分.
15.(本小题满分14分)
已知集合A表示函数 的值域,集合B表示函数
的值域,集合B表示函数
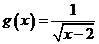 的定义域,集合C表示不等式
的定义域,集合C表示不等式 的解
的解
集.
(1)求集合A和B;
(2)若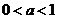 ,判断集合
,判断集合 与集合C的关系.
与集合C的关系.
16.(本小题满分14分)
已知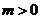 ,且向量
,且向量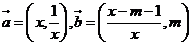 .
.
(1)
若向量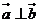 ,求
,求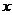 的值;
的值;
(2)
若向量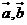 满足
满足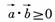 ,求实数
,求实数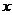 的取值范围.
的取值范围.
17.(本小题满分14分)
已知 ,
, .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
18.(本小题满分14分)
已知在一袋中有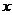 个红球、3个黑球和2个白球,现从中任取3个.
个红球、3个黑球和2个白球,现从中任取3个.
(1)如果 ,求取出的3球中颜色都相同的概率;
,求取出的3球中颜色都相同的概率;
(2)如果取出的3球的颜色各不相同的概率为 ,求
,求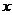 的值
的值
19.(本小题满分14分)
已知函数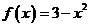 .
.
(1)求过点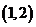 的切线方程;
的切线方程;
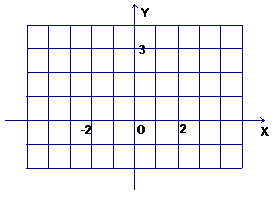
(2)在下面坐标系中作出函数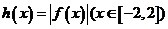 的图象;
的图象;
(3)若函数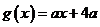 的图象总在函数
的图象总在函数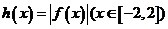 图象的上方,求实数
图象的上方,求实数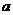 的取值范围.
的取值范围.
20.(本小题满分14分)已知正项数列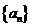 满足:
满足:
 .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)求数列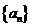 的通项
的通项 ;
;
(3)求证: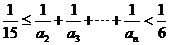 .
.
2006学年浙江省五校联考(一)
数学(文科)答题卷
试题
一
二
三
总分
15
16
17
18
19
20
得分
卷Ⅰ(选择题,共50分)
题目
1
2
3
4
5
6
7
8
9
10
卷Ⅱ(非选择题,共100分)
二、填空题:本大题共4小题,每小题4分,共16分.
11. 12.
13. 14.
三、解答题:本大题共6小题,每小题14分,共84分.
15.(本小题满分14分)
已知集合A表示函数 的值域,集合B表示函数
的值域,集合B表示函数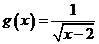 的定
的定
义域,集合C表示不等式 的解集.
的解集.
(1)求集合A和B;
(2)若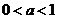 ,判断集合
,判断集合 与集合C的关系.
与集合C的关系.
16.(本小题满分14分)
已知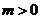 ,且向量
,且向量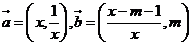 .
.
(3)
若向量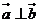 ,求
,求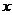 的值;
的值;
(2)若向量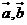 满足
满足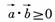 ,求实数
,求实数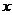 的取值范围.
的取值范围.
17.(本小题满分14分)
已知 ,
, .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
18.(本小题满分14分)
已知在一袋中有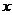 个红球、3个黑球和2个白球,现从中任取3个.
个红球、3个黑球和2个白球,现从中任取3个.
(1)如果 ,求取出的3球中颜色都相同的概率;
,求取出的3球中颜色都相同的概率;
(2)如果取出的3球的颜色各不相同的概率为 ,求
,求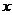 的值.
的值.
19.(本小题满分14分)
已知函数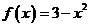 .
.
(1)求过点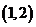 的切线方程;
的切线方程;
(2)在下面坐标系中作出函数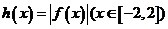 的图象;
的图象;
 (3)若函数
(3)若函数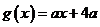 的图象总在函数
的图象总在函数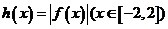 图象的上方,求实数
图象的上方,求实数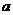 的取值范围.
的取值范围.
20.(本小题满分14分)已知正项数列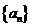 满足:
满足:
 .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)求数列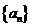 的通项
的通项 ;
;
(3)求证: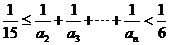 .
.
浙江省2006学年高三五校联考数学卷(文科)评分参考
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
C
C
A
B
D
B
D
A
二.填空题:
11. ; 12.
; 12. ;13.28; 14.
;13.28; 14.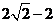 .
.
三.解答题:
15.(1)∵ ,∴
,∴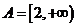 3分
3分
∵要使函数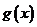 有意义,则
有意义,则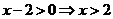 ∴
∴ 6分
6分
(2)∵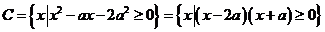 9分
9分
∵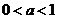
∴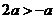
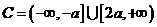 ,
12分
,
12分
又∵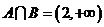
而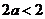
∴满足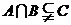 14分
14分
16.(1)∵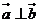 ,∴
,∴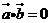
即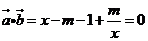
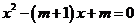 解得
解得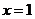 或
或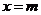 4分
4分
(2)因不等式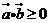 等价于
等价于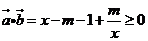

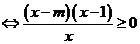 8分
8分
当 时,
时, 或
或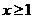 ;
10分
;
10分
当 时,
时, ;
12分
;
12分
当 时,
时, 或
或 .
14分
.
14分
17.(1)∵ ,∴
,∴ 2分
2分
∵ ,∴
,∴ ,
4分
,
4分
∴ .
6分
.
6分
(2)∵
又∵

∴ 14分
14分
18.(1)设3球中颜色都相同的事件为A
当 时,
时,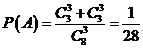 5分
5分
(2)设取出3球中颜色都不相同的事件为B,则有
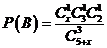
依题意有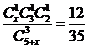
化简得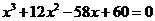
即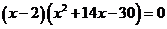
因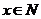 ,所以
,所以 14分
14分
19.(1)∵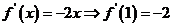 ,
,
∴过点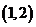 的切线方程为:
的切线方程为: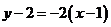 ,即
,即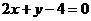 . 4分
. 4分
(2)在坐标系中标出主要的关键点,图象要求光滑美观. 8分
(3)方法1:把问题转化为不等式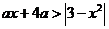 对一切
对一切 恒成立
恒成立
∵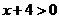
∴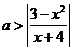 对一切
对一切 恒成立
恒成立
∵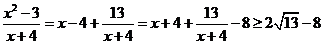 ,当且仅当
,当且仅当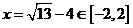 时取到等号,
时取到等号,
∴当且仅当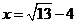 时,
时,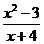 的最小值为
的最小值为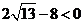
∵当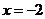 时,
时,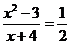 ,
,
∴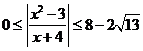
∴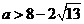 .
14分
.
14分
方法2:∵函数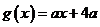 的图象恒过点
的图象恒过点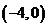 的直线,∴在
的直线,∴在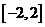 上,只要直线在函数
上,只要直线在函数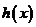 的图象的上方即可.
的图象的上方即可.
①如果直线与二次函数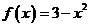 相切,
相切,
思路1:则由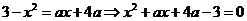 ,
,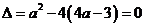
解得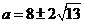 (验证得
(验证得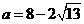 时,切点在第二象限)
时,切点在第二象限)
此时,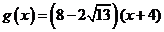 .
.
思路2: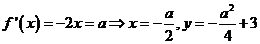 代入
代入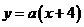
得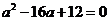 ,解得
,解得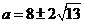 (验证得
(验证得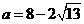 时,切点在第二象限)
时,切点在第二象限)
此时,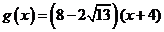 .
.
②如果直线过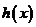 的左端点
的左端点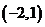 ,则
,则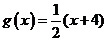 .
.
∵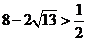 ,∴满足条件的实数
,∴满足条件的实数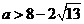 .
14分
.
14分
20.(1)∵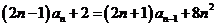
∴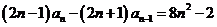
即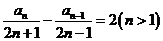
∵ ,∴
,∴ 是以1为首项,2为公差的等差数列 5分
是以1为首项,2为公差的等差数列 5分
(2)∵
∴ 9分
9分
(3)∵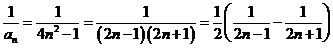
∴

∵ 在
在 上单调递增,
上单调递增,
∴当 时,即
时,即 ,另一方面
,另一方面 14分
14分