2007届高三数学小题训练(5)
姓名: 班级:
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题意要求的。
1.已知集合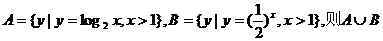 =( )
=( )
(A)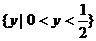 (B)
(B)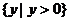
(C) (D)R
(D)R
2.在等差数列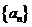 中,
中,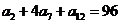 ,则
,则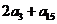 的值为……… ( )
的值为……… ( )
(A) 24 (B) 48 (C) 96 (D) 192
3、函数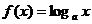 满足
满足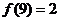 ,则
,则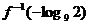 的值是………( )
的值是………( )
(A)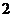 (B)
(B)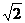 (C)
(C)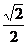 (D)
(D)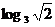
4、设f (x)=|2-x2|,若0<a<b且f (a)=f (b),则a+b的取值范围是
A.(0,2) B.(,2) C.(,4) D.(0,)
5.函数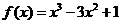 是减函数的区间为…………
( )
是减函数的区间为…………
( )
(A)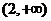 (B)
(B)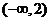 (C)
(C)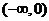 (D)
(D)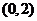
6.在数列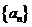 中,
中,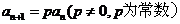 ,且前
,且前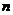 项和为
项和为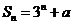 ,则实数
,则实数 为
为
(A)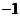 (B)
(B)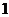 (C)
(C)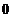 (D)
(D)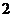
7、设 为偶函数,对于任意的
为偶函数,对于任意的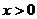 的数都有
的数都有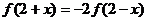 ,
,
已知 ,则
,则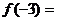 ……………………………………………( )
……………………………………………( )
(A)2 (B)-2 (C)8 (D)-8
8、函数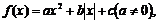 其定义域
其定义域 分成了四个单调区间,则实数
分成了四个单调区间,则实数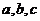 满足
满足
…………………………………………………………………… ( )
(A)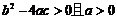 (B)
(B)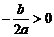 (C)
(C)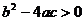 (D)
(D)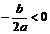
9、按如下方式定义函数 :对于每个实数
:对于每个实数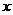 ,
, 的值为
的值为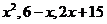 中的最小值.则
中的最小值.则 最大值为………………………………………………( )
最大值为………………………………………………( )
(A)4 (B)9 (C)16 (D)25
10..若函数f (x)=,则y=f (1-x)的图象可以是

第二卷(非选择题共100分)
二、填空题:本大题共6小题,每小题5分,共30分。把答案填在答题卷相应位置。
11、若函数f (3-2x)的定义域为(-1,2],则函数f (x)的定义域是
12.函数f(x)=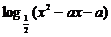 在
在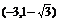 上单调递增,且值域为R,则a的取值范围是___________
上单调递增,且值域为R,则a的取值范围是___________
13.设函数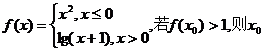 的取值范围为 .
的取值范围为 .
14.已知函数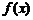 是定义在
是定义在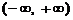 上的偶函数. 当
上的偶函数. 当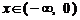 时,
时,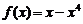 ,则当
,则当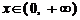 时,
时,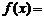
15、定义在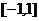 上的偶函数
上的偶函数 ,
,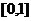 是
是 的增区间,则不等式
的增区间,则不等式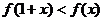 的解集是
的解集是
16.设f(x)是定义在R上的奇函数,且y=f (x)的图象关于直线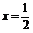 对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________.
对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________.
答案:
题号
1
2
3
4
5
6
7
8
9
10
答案
11、 12、 13、
14、 15、 16、
附加题:设关于x的一元二次方程ax2+x+1=0(a>0)有两个实根x1,x2.
(1)求(1+x1)(1+x2)的值;
(2)求证:x1<-1,且x2<-1;
(3)如果∈[,10],试求a的最大值.
2007届高三数学小题训练(5)答案
题号
1
2
3
4
5
6
7
8
9
10
答案
B
B
C
B
D
A
D
B
B
C
二、填空题
11、[-2,10) 12、[0,2]
13、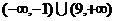 14、
14、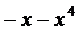
15、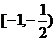 16、0
16、0
附加题:
(1) (1+x1)(1+x2)=1+(x1+x2)+x1x2=1-+=1;………………………………………4分
(2)证明:令f (x)=ax2+x+1,由△=1-
∴抛物线f (x)的对称轴x=-≤-2<-1,
又f(-1)=a>0,所以f(x)的图象与x轴的交点都在点(-1,0)的左侧,
故,x1<-1,且x2<-1; ………………………………………………………9分
(3)由(1)得,x1=-1=-
∴=-∈[,10],∴-∈[,].
而a==-=-[(-)-]2+,故当,-=时,a取得最大值为.……15分