2008年高考复习求解圆锥曲线问题易做易错题选
圆锥曲线是中学数学教学的重点内容之一,也是历届高考命题的热点,求解圆锥曲线问题时,学生应注意避免以下常见问题。
一、概念不清
例1 双曲线 上的点P到点(5,0)的距离为8.5,求点P到点(
上的点P到点(5,0)的距离为8.5,求点P到点( )的距离。
)的距离。
错解 设双曲线的两个焦点分别为 ,
, ,
,
由双曲线定义知
所以 或
或
剖析 由题意知,双曲线左支上的点到左焦点的最短距离为1,
所以 不合题意,事实上,在求解此类问题时,应灵活运用双曲线定义,分析出点P的存在情况,然后再求解。如本题中,因左顶点到右焦点的距离为9>8.5,故点P只能在右支上,所求
不合题意,事实上,在求解此类问题时,应灵活运用双曲线定义,分析出点P的存在情况,然后再求解。如本题中,因左顶点到右焦点的距离为9>8.5,故点P只能在右支上,所求
例2 已知圆 ,圆
,圆
 都内切于动圆,试求动圆圆心的轨迹方程。
都内切于动圆,试求动圆圆心的轨迹方程。
错解:圆O2:
即为
所以圆O2的圆心为 ,半径
,半径 ,
,
而圆 的圆心为
的圆心为 ,半径
,半径 ,
,
设所求动圆圆心M的坐标为(x,y),半径为r
则 且
且
所以
即
化简得
即 为所求动圆圆心的轨迹方程。
为所求动圆圆心的轨迹方程。
剖析:上述解法将 =3看成
=3看成 ,误认为动圆圆心的轨迹为双曲线,这是双曲线的概念不清所致。
,误认为动圆圆心的轨迹为双曲线,这是双曲线的概念不清所致。
事实上,| 表示动点M到定点
表示动点M到定点 及
及 的距离差为一常数3。
的距离差为一常数3。
且 ,点M的轨迹为双曲线右支,方程为
,点M的轨迹为双曲线右支,方程为

二、忽视隐含条件
例3 点P与定点F(2,0)的距离和它到直线x=8的距离比是1:3,求动点P与定点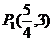 距离的最值。
距离的最值。
错解:设动点P(x,y)到直线x=8的距离为d,则
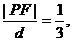
即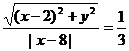
两边平方、整理得
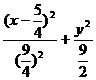 =1 (1)
=1 (1)
由此式可得:
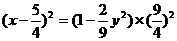
因为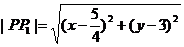
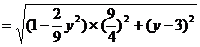
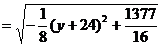
所以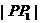
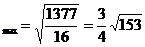
剖析 由上述解题过程知,动点P(x,y)在一椭圆上,由椭圆性质知,椭圆上点的横纵坐标都是有限制的,上述错解在于忽视了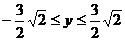 这一取值范围,由以上解题过程知,
这一取值范围,由以上解题过程知,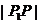 的最值可由二次函数在区间上的单调性给予解决
的最值可由二次函数在区间上的单调性给予解决
即:当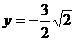 时,
时,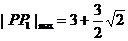
三、忽视元素之间的制约关系
例4 已知双曲线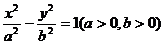 的离心率e=
的离心率e=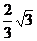 , 过点A(
, 过点A(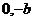 )和B(a,0)的直线与原点的距离为
)和B(a,0)的直线与原点的距离为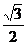 ,直线y=kx+m
,直线y=kx+m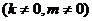 与该双曲线交于不同两点C、D,且C、D两点都在以A为圆心的同一圆上,求m 的取值范围。
与该双曲线交于不同两点C、D,且C、D两点都在以A为圆心的同一圆上,求m 的取值范围。
错解 由已知,有
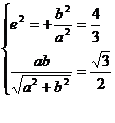
解之得: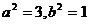
所以双曲线方程为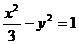
把直线 y=kx+m代入双曲线方程,并整理得:
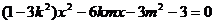
所以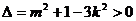 (1)
(1)
设CD中点为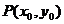 ,
,
则AP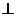 CD,且易知:
CD,且易知:
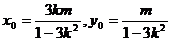
所以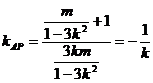
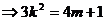 (2)
(2)
将(2)式代入(1)式得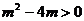
解得m>4或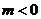
故所求m的范围是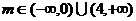
剖析 上述错解,在于在减元过程中,忽视了元素之间的制约关系,将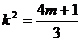 代入(1) 式时,m受k的制约。
代入(1) 式时,m受k的制约。
因为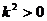
所以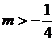
故所求m的范围应为
m>4或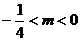
四、没有分类意识
例5 椭圆中心是坐标原点,长轴在x轴上,离心率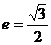 ,已知点P(
,已知点P(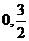 )到椭圆上的点最远距离是
)到椭圆上的点最远距离是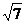 ,求这个椭圆的方程。
,求这个椭圆的方程。
错解 设所求椭圆方程为
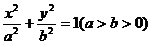
因为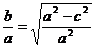
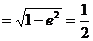
所以a=2b
于是椭圆方程为
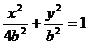
设椭圆上点M(x,y)到点P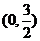 的距离为d,
的距离为d,
则: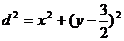
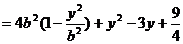
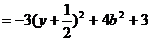
所以当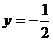 时,
时,
有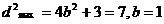
所以所求椭圆方程为
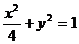
剖析 由椭圆方程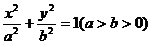
得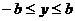
由(1)式知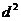 是y的二次函数,
是y的二次函数,
其对称轴为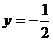
上述错解在于没有就对称轴在区间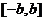 内或外进行分类,
内或外进行分类,
其正确应对f(y)=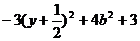 的最值情况进行讨论:
的最值情况进行讨论:
(1)当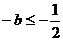 ,即
,即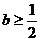 时
时
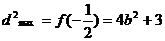 =7
=7
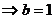 ,方程为
,方程为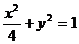
(2)当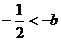 ,
,
即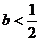 时,
时,
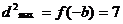
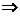
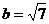
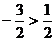 ,与
,与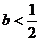 矛盾。
矛盾。
综上所述,所求椭圆方程为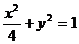
五、忽视判别式法。
例 6 已知双曲线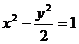 ,问过点A(1,1)能否作直线
,问过点A(1,1)能否作直线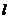 ,使
,使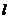 与双曲线交于P、Q两点,并且A为线段PQ的中点?若存在,求出直线
与双曲线交于P、Q两点,并且A为线段PQ的中点?若存在,求出直线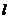 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
错解 设符合题意的直线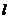 存在,并设
存在,并设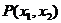 、
、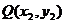
则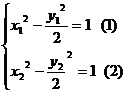
(1)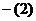 得
得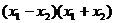
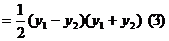
因为A(1,1)为线段PQ的中点,
所以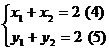
将(4)、(5)代入(3)得
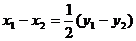
若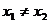 ,则直线
,则直线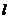 的斜率
的斜率
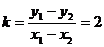
所以符合题设条件的直线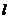 存在。
存在。
其方程为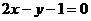
剖析 在(3)式成立的前提下,由(4)、(5)两式可推出(6)式,但由(6)式不能推出(4)(5)两式,故应对所求直线进行检验,上述错解没有做到这一点,故是错误的。
应在上述解题的基础上,再由
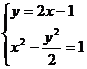
得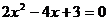
根据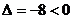 ,说明所求直线不存在。
,说明所求直线不存在。
六、忽视斜率不存在的情况。
例7 已知椭圆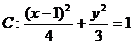 ,F为它的右焦点,直线
,F为它的右焦点,直线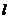 过原点交椭圆C于A、B两点。求
过原点交椭圆C于A、B两点。求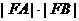 是否存在最大值或最小值?若不存在,说明理由。
是否存在最大值或最小值?若不存在,说明理由。
错解 设A、B两点坐标分别为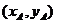 、
、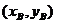
因为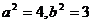
所以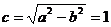
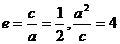
又椭圆中心为(1,0),右准线方程为x=5
所以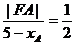
即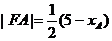
同理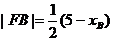
所以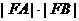
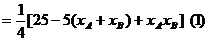
设直线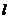 的方程为y=kx,代入椭圆方程得
的方程为y=kx,代入椭圆方程得
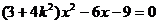
所以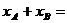
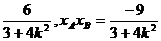
代入(1)式得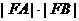
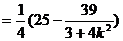
所以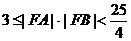
所以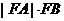 |有最小值3,无最大值。
|有最小值3,无最大值。
剖析 上述错解过程忽视了过原点斜率不存在的直线,当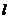 的斜率不存在时,有
的斜率不存在时,有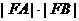
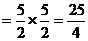
所以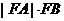 有最小值为 3,最大值为25/4
有最小值为 3,最大值为25/4