-
网址:http://m.1010jiajiao.com/paper/timu/5158825.html[举报]
10.在正三棱柱
 中,若
中,若 ,
, ,则点
,则点 到平面
到平面 的距离为( ) (A)
的距离为( ) (A) (B)
(B) (C)
(C) (D)
(D)
- 题目来源:08届高考理科数学第二次模拟测试试题2 数学(理科) 第Ⅰ卷 选择题(共60分)
(参考答案及评分细则)
一.选择题:DCADB DBAAB BC
二.填空题:13、 ,14、45,15、
,14、45,15、 16、②、③
16、②、③
三.解答题:
17.解:(Ⅰ)∵ 为奇函数,∴
为奇函数,∴
又 ,∴
,∴ …………………………………………(4分)
…………………………………………(4分)
(Ⅱ)y=x+cos3x+ =x+cos3x-sin3x=x+
=x+cos3x-sin3x=x+
∴y′=1+3 ,……………………………………(8分)
,……………………………………(8分)
又∵x∈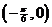 ,∴
,∴ ∈
∈
则y′∈(-2,4) ………………………………………………(12分)
18.解:(Ⅰ)P(ξ=0)= =
=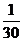 ,P(ξ=1)=
,P(ξ=1)= ,
,
P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)= .……………………(3分)
.……………………(3分)
|
ξ |
0 |
1 |
2 |
3 |
|
P |
 |
 |
 |
 |
∴
则:Eξ=0× +1×
+1× +2×
+2× +3×
+3× =
= ……………………………(6分)
……………………………(6分)
(Ⅱ)甲未通过的概率为:p1= ……………………(8分)
……………………(8分)
乙未通过的概率为:p2= ……………………………(10分)
……………………………(10分)
∴甲、乙两人至少有一人通过面试的概率为: =
= …(12分)
…(12分)
19.(1)略(2) (3)arccos
(3)arccos
20.解: 由 求导数得
求导数得 ,过y=f(x)上点P(1,f(1))处的切线方程为:
,过y=f(x)上点P(1,f(1))处的切线方程为: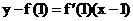 即y-(a+b+c+1)=(3+2a+b)(x-1),而过y=f(x)上P(1,f(1))的切线方程为:y=3x+1,故
即y-(a+b+c+1)=(3+2a+b)(x-1),而过y=f(x)上P(1,f(1))的切线方程为:y=3x+1,故 即
即

 y=f(x)在x=-2时有极值,故
y=f(x)在x=-2时有极值,故

由 相联立解得
相联立解得 ,
,
(2) 在区间
在区间 上单调递增
上单调递增
又 ,由(1)知
,由(1)知

依题意 在
在 上恒有
上恒有 ,即
,即 在
在 上恒成立.
上恒成立.
①在
|
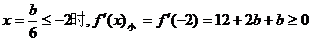

③在
综合上述讨论可知,所求参数b取值范围是:b≥0……(14分)
21.解:(1)由题意知: ,同理可得:
,同理可得: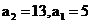
(2)假设存在实数 符合题意,,则
符合题意,,则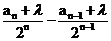 必为与n无关的常数,
必为与n无关的常数,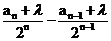 =
= ,故
,故
(3)由(2)知数列 的公差d=1,得
的公差d=1,得 ,用错位相减法得:
,用错位相减法得:
22.解:(1)由对称性,不妨设M是右准线 与一渐近线
与一渐近线 的交点,其坐标为M(
的交点,其坐标为M( ),
),
 ∴
∴ ,又
,又 ∴
∴ ,
, ,解得
,解得 ,所以双曲线C的方程是
,所以双曲线C的方程是 ;
(6分)
;
(6分)
(2)设直线l的斜率为k,则l的方程为y=kx+1,点
由 得:
得:
 l与双曲线C的右支交于不同的两点P、Q,∴
l与双曲线C的右支交于不同的两点P、Q,∴
∴ 且
且 ①
(10分)
①
(10分)
又
 且P在A、Q之间,
且P在A、Q之间, ,∴
,∴ 且
且 ,
,
∴ ∴
∴ ,
,

= 在
在 上是减函数(
上是减函数(
 ),∴
),∴ ,∴
,∴
 ,由于
,由于 ,∴
,∴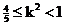 ② (12分)
② (12分)
由①②可得: ,即直线l斜率取值范围为
,即直线l斜率取值范围为 (14分)
(14分)
