-
网址:http://m.1010jiajiao.com/paper/timu/5158407.html[举报]
14. 解:(1)由
 消去y得:
消去y得: ①
设
①
设 ,问题(1)化为方程①在x∈(-a,a)上有唯一解或等根.
只需讨论以下三种情况:
1°△=0得:
,问题(1)化为方程①在x∈(-a,a)上有唯一解或等根.
只需讨论以下三种情况:
1°△=0得: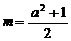 ,此时xp=-a2,当且仅当-a<-a2<a,即0<a<1时适合;
2°f (a)f
(-a)<0,当且仅当-a<m<a;
3°f (-a)=0得m=a,此时xp=a-2a2,当且仅当-a<a-2a2<a,即0<a<1时适合.
f (a)=0得m=-a,此时xp=-a-2a2,由于-a-2a2<-a,从而m≠-a.
综上可知,当0<a<1时,
,此时xp=-a2,当且仅当-a<-a2<a,即0<a<1时适合;
2°f (a)f
(-a)<0,当且仅当-a<m<a;
3°f (-a)=0得m=a,此时xp=a-2a2,当且仅当-a<a-2a2<a,即0<a<1时适合.
f (a)=0得m=-a,此时xp=-a-2a2,由于-a-2a2<-a,从而m≠-a.
综上可知,当0<a<1时,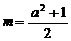 或-a<m≤a;
当a≥1时,-a<m<a.……………………………………………… 10分
或-a<m≤a;
当a≥1时,-a<m<a.……………………………………………… 10分(2)△OAP的面积
 ∵0<a<
∵0<a< ,故-a<m≤a时,0<
,故-a<m≤a时,0< <a,
由唯一性得
<a,
由唯一性得  显然当m=a时,xp取值最小.由于xp>0,从而yp=
显然当m=a时,xp取值最小.由于xp>0,从而yp=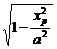 取值最大,此时
取值最大,此时 ,∴
,∴ .
当
.
当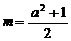 时,xp=-a2,yp=
时,xp=-a2,yp= ,此时
,此时 .
下面比较
.
下面比较 与
与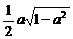 的大小:
令
的大小:
令 ,得
,得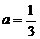 故当0<a≤
故当0<a≤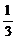 时,
时, ≤
≤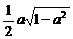 ,此时
,此时 .
当
.
当 时,
时,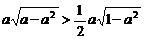 ,此时
,此时 .……… 20分
.……… 20分 - 题目来源:08届高考数学解析几何综合练习二