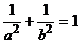-
网址:http://m.1010jiajiao.com/paper/timu/5158406.html[举报]
13.利用极坐标解决:以坐标原点为极点,x轴为极轴建立极坐标系,则椭圆的极坐标方程为
 ------(1)
------(1)显知此平行四边形ABCD必为菱形,设A
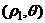 ,则B
,则B
代入(1)式相加:
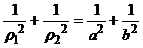
由于该菱形必与单位圆相切,故原点到AB的距离为1,
∴
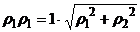 ,从而
,从而 ,∴
,∴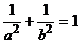
- 题目来源:08届高考数学解析几何综合练习二
网址:http://m.1010jiajiao.com/paper/timu/5158406.html[举报]
13.利用极坐标解决:以坐标原点为极点,x轴为极轴建立极坐标系,则椭圆的极坐标方程为 ------(1)
------(1)
显知此平行四边形ABCD必为菱形,设A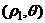 ,则B
,则B
代入(1)式相加: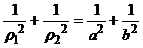
由于该菱形必与单位圆相切,故原点到AB的距离为1,
∴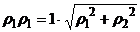 ,从而
,从而 ,∴
,∴