-
1.在△OAB中,O为坐标原点,
 ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时, ( D )
( D )A.
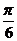 B.
B. C.
C. D.
D.
-
2. “a=b”是“直线
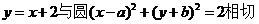 ”的 (A )
”的 (A )A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
-
3. 圆(x+2)2+y2=5关于原点(0,0)对称的圆的方程为 (A )
(A) (x-2)2+y2=5; (B) x2+(y-2)2=5;
(C) (x+2)2+(y+2)2=5; (D) x2+(y+2)2=5。
4 点(1,-1)到直线x-y+1=0的距离是( D )
(A)
 (B)
(B)  (C)
(C)  (D)
(D)
-
5.设集合A={(x,y)|x,y,1-x-y是三角形的三边长},则A所表示的平面区域(不含边界的阴影部分)是( A )
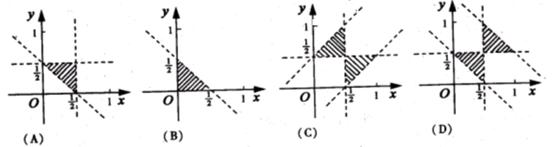
5将直线2x-y+λ=0,沿x轴向左平移1个单位,所得直线与圆x2+y2+2x-4y=0相切,则实数λ的值为 (A)
A.-3或7 B.-2或8 C.0或10 D.1或11
6在坐标平面上,不等式组
 所表示的平面区域的面积为(C )
所表示的平面区域的面积为(C )(A)
 (B)
(B) (C)
(C)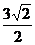 (D)2
(D)2 -
7. 设直线
 过点
过点 ,且与圆
,且与圆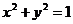 相切,则
相切,则 的斜率是( C )
的斜率是( C )(A)
 (B)
(B)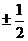 (C)
(C) (D)
(D)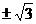
-
8. 已知直线
 过点
过点 ,当直线
,当直线 与圆
与圆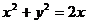 有两个交点时,其斜率k的取值范围是(B )
有两个交点时,其斜率k的取值范围是(B )(A)
 (B)
(B)
(C)
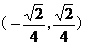 (D)
(D)
-
9.已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为(B)
(A)0 (B)-8 (C)2 (D)10
10从原点向圆 x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为(B )
(A)π (B)2π (C)4π (D)6π
11若直线
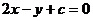 按向量
按向量 平移后与圆
平移后与圆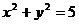 相切,则c的值为( A )
相切,则c的值为( A )A.8或-2 B.6或-4 C.4或-6 D.2或-8
-
12.设直线的方程是
 ,从1,2,3,4,5这五个数中每次取两个不同的数作为A、 B的值,则所得不同直线的条数是 (C )
,从1,2,3,4,5这五个数中每次取两个不同的数作为A、 B的值,则所得不同直线的条数是 (C )A.20 B.19 C.18 D.16
-
13.已知点P(x,y)在不等式组
 表示的平面区域上运动,则z=x-y的取值范围是 ( C )
表示的平面区域上运动,则z=x-y的取值范围是 ( C ) A.[-2,-1] B.[-2,1] C.[-1,2] D.[1,2]
-
14.“m=
 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的(B )
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的(B )(A)充分必要条件 (B)充分而不必要条件
(C)必要而不充分条件 (D)既不充分也不必要条件
填空题
-
1.圆心为
 且与直线
且与直线 相切的圆的方程为
相切的圆的方程为 .
. -
2.设直线
 和圆
和圆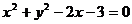 相交于点A、B,则弦AB的垂直平分线方程是
相交于点A、B,则弦AB的垂直平分线方程是  .
. -
3.已知直线ax+by+c=0与圆O:x2+y2=1相交于A、B两点,且|AB|=
 ,则
,则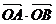 =
=  .
. -
4.某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元. 在满足需要的条件下,最少要花费 500 元.
-
5.非负实数x、y满足
 的最大值为 9 .
的最大值为 9 .6设实数x, y满足

 .
. -
7.
 若x,y满足条件
x+y≤3
若x,y满足条件
x+y≤3y≤2x ,则z=3x+4y的最大值是 11 .
8直线y=
 x关于直线x=1对称的直线方程是 x+2y-2=0
.
x关于直线x=1对称的直线方程是 x+2y-2=0
. -
9.将参数方程
 (
( 为参数)化为普通方程,所得方程是_ (x-1)2+y2=4
_________。
为参数)化为普通方程,所得方程是_ (x-1)2+y2=4
_________。 -
10.设
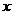 、
、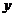 满足约束条件
满足约束条件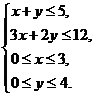 则使得目标函数
则使得目标函数 的最大的点
的最大的点 是(2,3).
是(2,3).解答题
-
1.
 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得
如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得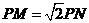 试建立适当的坐标系,并求动点 P的轨迹方程.
试建立适当的坐标系,并求动点 P的轨迹方程.解:如图,以直线
 为
为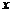 轴,线段
轴,线段 的垂直平分线为
的垂直平分线为 轴,建立平面直角坐标系,则两圆心分别为
轴,建立平面直角坐标系,则两圆心分别为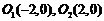 .设
.设 ,则
,则 ,同理
,同理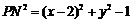 .
.∵
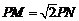 ,
,∴
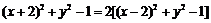 ,
,即
 ,即
,即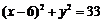 .这就是动点
.这就是动点 的轨迹方程.
的轨迹方程. -
2.(广东卷)在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图5所示).将矩形折叠,使A点落在线段DC上.
(Ⅰ)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
(Ⅱ)求折痕的长的最大值.


.解(I) (1)当
 时,此时A点与D点重合, 折痕所在的直线方程
时,此时A点与D点重合, 折痕所在的直线方程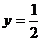
(2)当
 时,将矩形折叠后A点落在线段CD上的点为G(a,1)
时,将矩形折叠后A点落在线段CD上的点为G(a,1)所以A与G关于折痕所在的直线对称,有

故G点坐标为
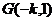 ,从而折痕所在的直线与OG的交点坐标(线段OG的中点)为
,从而折痕所在的直线与OG的交点坐标(线段OG的中点)为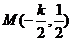
折痕所在的直线方程
 ,即
,即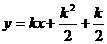
由(1)(2)得折痕所在的直线方程为:
k=0时,
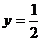 ;
; 时
时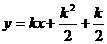
(II)(1)当
 时,折痕的长为2;
时,折痕的长为2;(1) 当
 时, 折痕所在的直线与坐标轴的交点坐标为
时, 折痕所在的直线与坐标轴的交点坐标为
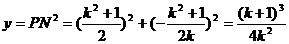

令
 解得
解得 ∴
∴
所以折痕的长度的最大值2