网址：http://m.1010jiajiao.com/paper/timu/5158066.html[举报]

2.(广东卷)在平面直角坐标系中，已知矩形ABCD的长为2，宽为1，AB、AD边分别在x轴、y轴的正半轴上，A点与坐标原点重合(如图5所示)．将矩形折叠，使A点落在线段DC上．

(Ⅰ)若折痕所在直线的斜率为k，试写出折痕所在直线的方程；

(Ⅱ)求折痕的长的最大值．

.解(I) (1)当时,此时A点与D点重合, 折痕所在的直线方程

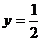
(2)当时，将矩形折叠后A点落在线段CD上的点为G(a,1)

所以A与G关于折痕所在的直线对称，有

故G点坐标为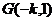，从而折痕所在的直线与OG的交点坐标(线段OG的中点)为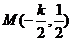

折痕所在的直线方程，即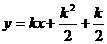

由(1)(2)得折痕所在的直线方程为：

k=0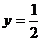时，；时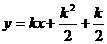

(II)(1)当时，折痕的长为2;

(1)　　 当时, 折痕所在的直线与坐标轴的交点坐标为

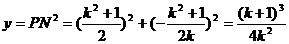
令解得　　 ∴

所以折痕的长度的最大值2