-
1、斜率为1的直线l与椭圆
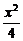 +y2=1相交于A、B两点,则|AB|的最大值为
( )
+y2=1相交于A、B两点,则|AB|的最大值为
( )A.2 B.
 C.
C.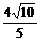 D.
D.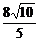
-
2、抛物线y=ax2与直线y=kx+b(k≠0)交于A、B两点,且此两点的横坐标分别为x1,x2,直线与x轴交点的横坐标是x3,则恒有 ( )
A.x3=x1+x2 B.x1x2=x1x3+x2x3 C.x1+x2+x3=0 D.x1x2+x2x3+x3x1=0
-
3、过点(3,0)的直线l与双曲线4x2-9y2=36只有一个公共点,则直线l共有 ( )
(A)1条 (B)2条 (C)3条 (D)4条
-
4、设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是 ( )
A.[-
 ,
, ]
B.[-2,2] C.[-1,1] D.[-4,4]
]
B.[-2,2] C.[-1,1] D.[-4,4] -
5、若动点(x,y)在曲线
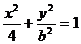 (b>0)上变化,则x22y的最大值为 ( )
(b>0)上变化,则x22y的最大值为 ( )(A)
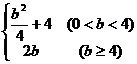 ; (B)
; (B) 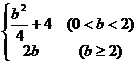 ; (C)
; (C) 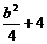 ;(D) 2b。
;(D) 2b。 -
6、已知双曲线
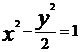 的焦点为F1、F2,点M在双曲线上且
的焦点为F1、F2,点M在双曲线上且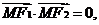 则点M到x轴的距离为(
)
则点M到x轴的距离为(
)(A)
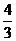 (B)
(B)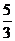 (C)
(C)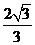 (D)
(D)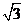
-
7、已知F1、F2是双曲线
 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 (
)
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 (
)A.
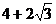 B.
B.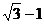 C.
C.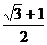 D.
D.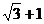
-
8、已知双曲线
 -
-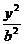 =1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为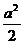 (O为原点),则两条渐近线的夹角为 ( )
(O为原点),则两条渐近线的夹角为 ( )A.30º B.45º C.60º D.90º
-
9、从集合{1,2,3…,11}中任选两个元素作为椭圆方程
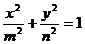 中的m和n,则能组成落在矩形区域B={(x,y)| |x|<11且|y|<9}内的椭圆个数为 ( )
中的m和n,则能组成落在矩形区域B={(x,y)| |x|<11且|y|<9}内的椭圆个数为 ( ) A.43 B. 72 C. 86 D. 90
-
10、设直线
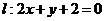 关于原点对称的直线为
关于原点对称的直线为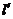 ,若
,若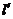 与椭圆
与椭圆 的交点为A、B,点
的交点为A、B,点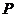 为椭圆上的动点,则使
为椭圆上的动点,则使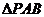 的面积为
的面积为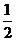 的点
的点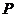 的个数为( )
的个数为( )(A)1 (B)2 (C)3 (D)4
-
11、直角坐标平面xoy中,若定点A(1,2)与动点P(x,y)满足
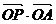 =4。则点P的轨迹方程是
.
=4。则点P的轨迹方程是
. -
12、如果过两点
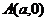 和
和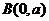 的直线与抛物线
的直线与抛物线 没有交点,那么实数
没有交点,那么实数 的取值范围是__________________.
的取值范围是__________________. -
13、在抛物线y2=16x内,通过点(2,1)且在此点被平分的弦所在直线的方程是_________.
-
14、正方形ABCD的边AB在直线y=x+4上,C、D两点在抛物线y2=x上,则正方形ABCD的面积为_________.
-
15、过双曲线
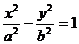 (a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_______.
(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_______. -
16、已知两点M(1,
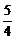 )、N(-4,-
)、N(-4,-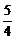 ),给出下列曲线方程:①4x+2y-1=0,②x2+y2=3,③
),给出下列曲线方程:①4x+2y-1=0,②x2+y2=3,③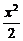 +y2=1,④
+y2=1,④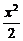 -y2=1,在曲线上存在点P满足|MP|=|NP|的所有曲线方程是_________.
-y2=1,在曲线上存在点P满足|MP|=|NP|的所有曲线方程是_________. -
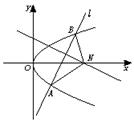
17、已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,且|AB|≤2p.
(1)求a的取值范围.
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
-
18、已知中心在原点,顶点A1、A2在x轴上,离心率e=
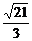 的双曲线过点P(6,6).
的双曲线过点P(6,6).(1)求双曲线方程.
(2)动直线l经过△A1PA2的重心G,与双曲线交于不同的两点M、N,问:是否存在直线l,使G平分线段MN,证明你的结论.
-
19、已知双曲线C的两条渐近线都过原点,且都以点A(
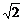 ,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.(1)求双曲线C的方程.
(2)设直线l过点A,斜率为k,当0<k<1时,双曲线C的上支上有且仅有一点B到直线l的距离为
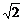 ,试求k的值及此时B点的坐标.
,试求k的值及此时B点的坐标. -
20、点A、B分别是椭圆
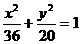 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于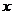 轴上方,
轴上方,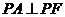 。
。(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于
 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离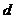 的最小值。
的最小值。 -
21、
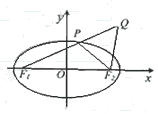
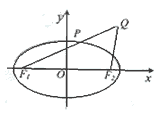 已知椭圆
已知椭圆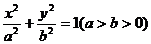 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足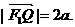 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足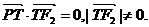
(Ⅰ)设
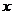 为点P的横坐标,证明
为点P的横坐标,证明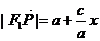 ;
;(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,
使△F1MF2的面积S=
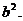 若存在,求∠F1MF2
若存在,求∠F1MF2的正切值;若不存在,请说明理由.
[2006年高考二轮复习专题讲义之针对训练]
解析几何专题--解析几何的综合运用同步训练答案
-
C B C C A C D D B B
-
11、x+2y-4=0 12、 13、y=8x-15. 14、18或50 15、2 16、
-
17、解:(1)设直线l的方程为:y=x-a,代入抛物线方程得(x-a)2=2px,即x2-2(a+p)x+a2=0
∴|AB|=
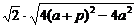 ≤2p.∴4ap+2p2≤p2,即4ap≤-p2
≤2p.∴4ap+2p2≤p2,即4ap≤-p2又∵p>0,∴a≤-
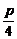 .
.(2)设A(x1,y1)、B(x2,y2),AB的中点 C(x,y),
由(1)知,y1=x1-a,y2=x2-a,x1+x2=2a+2p,
则有x=
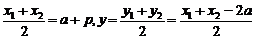 =p.
=p.∴线段AB的垂直平分线的方程为y-p=-(x-a-p),从而N点坐标为(a+2p,0)
点N到AB的距离为
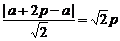
从而S△NAB=
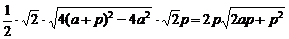
当a有最大值-
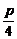 时,S有最大值为
时,S有最大值为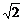 p2.
p2. -
18、解:(1)如图,设双曲线方程为
 =1.由已知得
=1.由已知得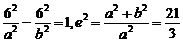 ,解得a2=9,b2=12.
,解得a2=9,b2=12.
所以所求双曲线方程为
 =1.
=1.(2)P、A1、A2的坐标依次为(6,6)、(3,0)、(-3,0),
∴其重心G的坐标为(2,2)
假设存在直线l,使G(2,2)平分线段MN,设M(x1,y1),N(x2,y2).则有
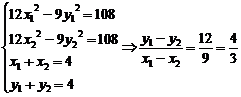 ,∴kl=
,∴kl=
∴l的方程为y=
 (x-2)+2,
(x-2)+2,由
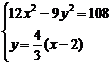 ,消去y,整理得x2-4x+28=0.
,消去y,整理得x2-4x+28=0.∵Δ=16-4×28<0, ∴所求直线l不存在.
-
19、解:(1)设双曲线的渐近线为y=kx,由d=
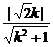 =1,解得k=±1.
=1,解得k=±1.即渐近线为y=±x,又点A关于y=x对称点的坐标为(0,
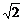 ).
).∴a=
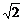 =b,所求双曲线C的方程为x2-y2=2.
=b,所求双曲线C的方程为x2-y2=2.(2)设直线l:y=k(x-
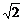 )(0<k<1
)(0<k<1 ,依题意B点在平行的直线l′上,
,依题意B点在平行的直线l′上,且l与l′间的距离为
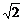 .
.设直线l′:y=kx+m,应有
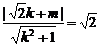 ,化简得m2+2
,化简得m2+2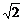 km=2.
②
km=2.
②把l′代入双曲线方程得(k2-1)x2+2mkx+m2-2=0,
由Δ=4m2k2-4(k2-1)(m2-2)=0.可得m2+2k2=2 ③
②、③两式相减得k=
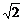 m,代入③得m2=
m,代入③得m2=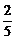 ,解设m=
,解设m= ,k=
,k= ,
,此时x=
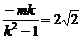 ,y=
,y=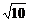 .故B(2
.故B(2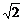 ,
,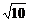 ).
). -
20、 [解](1)由已知可得点A(-6,0),F(0,4)
设点P(
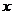 ,
,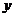 ),则
),则 ={
={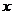 +6,
+6, 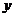 },
},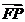 ={
={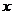 -4,
-4, 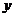 },由已知可得
},由已知可得
则2
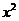 +9
+9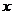 -18=0,
-18=0, 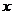 =
=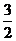 或
或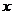 =-6.
=-6.由于
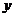 >0,只能
>0,只能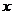 =
=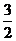 ,于是
,于是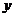 =
=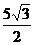 .
.∴点P的坐标是(
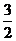 ,
,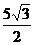 )
)(2) 直线AP的方程是
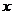 -
-
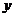 +6=0.
+6=0.设点M(
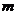 ,0),则M到直线AP的距离是
,0),则M到直线AP的距离是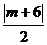 .
.于是
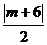 =
=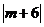 ,又-6≤
,又-6≤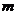 ≤6,解得
≤6,解得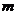 =2.
=2.椭圆上的点(
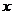 ,
,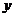 )到点M的距离
)到点M的距离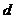 有
有 ,
,由于-6≤
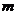 ≤6, ∴当
≤6, ∴当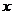 =
=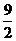 时,d取得最小值
时,d取得最小值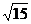
-
21、
 (Ⅰ)证法一:设点P的坐标为
(Ⅰ)证法一:设点P的坐标为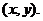
由P
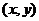 在椭圆上,得
在椭圆上,得
由
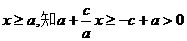 ,所以
,所以
 ………………………3分
………………………3分证法二:设点P的坐标为
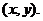 记
记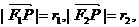
则
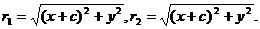
由
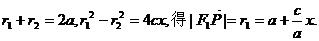
证法三:设点P的坐标为
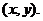 椭圆的左准线方程为
椭圆的左准线方程为
由椭圆第二定义得
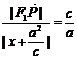 ,即
,即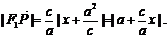
由
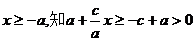 ,所以
,所以 …………………………3分
…………………………3分(Ⅱ)解法一:设点T的坐标为
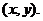
当
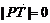 时,点(
时,点( ,0)和点(-
,0)和点(- ,0)在轨迹上.
,0)在轨迹上.当|
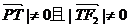 时,由
时,由 ,得
,得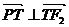 .
.又
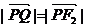 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.在△QF1F2中,
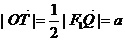 ,所以有
,所以有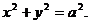
综上所述,点T的轨迹C的方程是
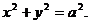 …………………………7分
…………………………7分解法二:设点T的坐标为
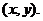 当
当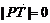 时,点(
时,点( ,0)和点(-
,0)和点(- ,0)在轨迹上.
,0)在轨迹上.当|
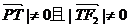 时,由
时,由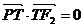 ,得
,得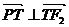 .
.又
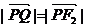 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点. 设点Q的坐标为(
 ),则
),则
因此
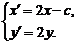 ①
①由
 得
得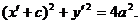 ②
②将①代入②,可得
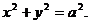
综上所述,点T的轨迹C的方程是
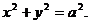 ……………………7分
……………………7分
(Ⅲ)解法一:C上存在点M(③
④
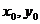 )使S=
)使S=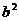 的充要条件是
的充要条件是
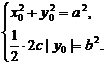
由③得
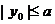 ,由④得
,由④得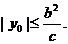 所以,当
所以,当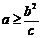 时,存在点M,使S=
时,存在点M,使S=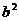 ;
;当
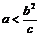 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分当
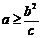 时,
时,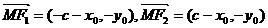 ,
,由
 ,
, ,
,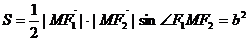 ,得
,得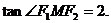
解法二:C上存在点M(
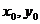 )使S=
)使S=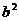 的充要条件是
的充要条件是③
④
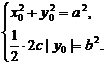
由④得
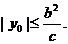 上式代入③得
上式代入③得
于是,当
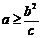 时,存在点M,使S=
时,存在点M,使S=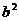 ;
;当
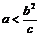 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分当
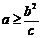 时,记
时,记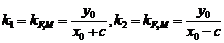 ,
,由
 知
知 ,所以
,所以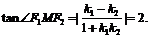 …………14分
…………14分