-
1.下列函数不属于二次函数的是……………………………………………………………( )
A.y=(x-1)(x+2) B.y=
 (x+1)2 C.y=2(x+3)2-2x2 D.y=1-
(x+1)2 C.y=2(x+3)2-2x2 D.y=1- x2
x2 -
2.下列函数中,当x>0时,y随x的增大而减小的是…………………………………………( )
A.
 B.
B. C.
C. D.
D.
-
3.二次函数
 的图象开口向下,则
的图象开口向下,则 的取值范围是 … ( )
的取值范围是 … ( )A.
 ≤
≤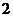 B.
B. <
<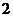 C.
C. ≥
≥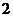 D.
D. >
>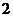
-
4.抛物线y=x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为………………………………………………………………………………… ( )
A.y=x2+4x+3 B. y=x2+4x+5 C. y=x2-4x+3 D.y=x2-4x-5
-
5.如图,夏季的一天,身高为1.6m的小玲想测量一下屋前大树的
 高度,她沿着树影BA由B到A
高度,她沿着树影BA由B到A 走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为………………………………………………………( )
走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为………………………………………………………( )A.8
 m B.6.4m C.4.8m D.10m
m B.6.4m C.4.8m D.10m
-
6.如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有…………………( )
A.7对; B.6对; C.5对; D. 4对



第5题 第6题
-
7.如图,P是Rt△ABC的斜边BC上异于B,C的一点,过P作
 直线截△ABC,使截得的三角形与△ABC
直线截△ABC,使截得的三角形与△ABC 相似,满足这样条件的直线共有(
)
相似,满足这样条件的直线共有(
) A.1条 B.2条
 C.3条
D.4条
C.3条
D.4条 -
8. .如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5
 ,CD =3,DE =4,则BF的长为( )
,CD =3,DE =4,则BF的长为( ) A.

 B.
B.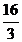 C.
C.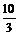
 D.
D.
-
9. 如图,四边形ABCD的对角线AC.BD相交于点O,且将这个四边形分成四个三角形,若
 ,则下列结论中一定正确的是
,则下列结论中一定正确的是A.1和2相似 B.1和3相似
C.1和4相似 D.2和4相似
 第9题图
第9题图

-
10.如图所示,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是………………………………………………………………………………………[ ]

-
11. 4与9的比例中项是______ .
-
12. 若
 是二次函数,则
是二次函数,则
 。
。 -
13.
 如图,在平行四边形
如图,在平行四边形 中,点
中,点 在
在 边上,且
边上,且 ,
, 与
与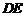 相交于点
相交于点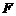 ,若
,若 ,则
,则

.
-
14. 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法:
①abc>0; ②a-b+c<0; ③3a+c<0; ④当-1<x<3时,y>0. 其中正确的结论是____ .
-
15. 已知

 ,求
,求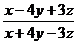 的值.
的值.解:
-
6. 用配方法求二次函数
 的对称轴、顶点坐标和最值。
的对称轴、顶点坐标和最值。解:
-
17. 已知二次函数图像的顶点坐标为(1,-1),且经过原点(0,0),求该函数的解析式。
解:
-
18. 如图,如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:
(1)将△ABC先向右平移4个单位,再向上平移1个
 单位,得到△A1B1C1;
单位,得到△A1B1C1;(2)以图中的点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.


-
19. 如图函数
 的图象与函数
的图象与函数 (x>0)的图象交于A、B两点,与y轴交于C点.已知A点的坐标为(2,1),C点坐标为(0,3).
(x>0)的图象交于A、B两点,与y轴交于C点.已知A点的坐标为(2,1),C点坐标为(0,3). (1)求函数
(1)求函数 的表达式和B点坐标;
的表达式和B点坐标;[解]
(2)观察图象,比较当x>0时,
 和
和 的大小.
的大小.B
 20. 如图,M为线段AB的中点,AE与BD交于点C,
20. 如图,M为线段AB的中点,AE与BD交于点C,
∠DME=∠A=∠B=α,且DM交AC于F,ME交
 BC于G.
BC于G.写出图中三对
 相似三角形,并证明其中的一对;
相似三角形,并证明其中的一对;[证]
.
-
21.甲、乙两家商场进行促销活动,甲商场采用“慢200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;……,乙商场按顾客购买商品的总金额打6折促销。
(1)若顾客在甲商场购买了510元的商品,付款时应付多少钱
 ?
?解:
(2)若顾客在甲商场购买商品的总金额为x(400≤x<600)元,优惠后得到商家的优惠率为p(p=
 ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;解:
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(200≤x<400)元,你认为选择哪家商场购买商品花钱较少?请说明理由。
解:

-
22.
 如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC=a、AC=b、AB=c.
如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC=a、AC=b、AB=c.(1)求线段BG的长;
解:
(2)求证:DG平分∠EDF;
证:
 (3)连接CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG.
(3)连接CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG.证:
-
23.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m
 ,球场的边界距O点的水平距离为18m。
,球场的边界距O点的水平距离为18m。(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。
