15. 如图,将小砝码至于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为M和m,各接触面间的动摩擦因数均为μ,砝码与纸板左端的距离及桌面右端的距离均为d.现用水平向右的恒定拉力F拉动纸板,下列说法正确的是( )
如图,将小砝码至于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为M和m,各接触面间的动摩擦因数均为μ,砝码与纸板左端的距离及桌面右端的距离均为d.现用水平向右的恒定拉力F拉动纸板,下列说法正确的是( )
 如图,将小砝码至于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为M和m,各接触面间的动摩擦因数均为μ,砝码与纸板左端的距离及桌面右端的距离均为d.现用水平向右的恒定拉力F拉动纸板,下列说法正确的是( )
如图,将小砝码至于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为M和m,各接触面间的动摩擦因数均为μ,砝码与纸板左端的距离及桌面右端的距离均为d.现用水平向右的恒定拉力F拉动纸板,下列说法正确的是( )| A. | 纸板相对砝码运动时,纸板所受摩擦力的大小为μ(M+m)g | |
| B. | 要使纸板相对砝码运动,F一定大于2μ(M+m)g | |
| C. | 若砝码与纸板分离时的速度小于$\sqrt{μgd}$,砝码不会从桌面上掉下 | |
| D. | 当F=μ(2M+4m)g时,砝码恰好到达桌面边缘 |
14.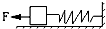 如图所示,物体重为100N,放在水平面上,物体右端与一轻弹簧连接,物体与地面的最大静摩擦力为40N,用一水平向左的30N的力作用于物体时,物体保持静止.则物体所受弹簧的弹力大小可能是( )
如图所示,物体重为100N,放在水平面上,物体右端与一轻弹簧连接,物体与地面的最大静摩擦力为40N,用一水平向左的30N的力作用于物体时,物体保持静止.则物体所受弹簧的弹力大小可能是( )
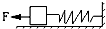 如图所示,物体重为100N,放在水平面上,物体右端与一轻弹簧连接,物体与地面的最大静摩擦力为40N,用一水平向左的30N的力作用于物体时,物体保持静止.则物体所受弹簧的弹力大小可能是( )
如图所示,物体重为100N,放在水平面上,物体右端与一轻弹簧连接,物体与地面的最大静摩擦力为40N,用一水平向左的30N的力作用于物体时,物体保持静止.则物体所受弹簧的弹力大小可能是( )| A. | 20N | B. | 40N | C. | 60N | D. | 80N |
13.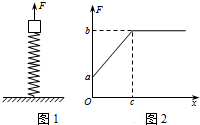 如图1所示,一轻弹簧下端固定在水平面上,上端放置一小物体,小物体处于静止状态.现对小物体施一竖直向上的拉力F,使小物体向上做匀加速直线运动,拉力F与物体位移x的关系如图2所示,a、b、c均为已知量,重力加速度为g,弹簧始终在弹性限度内.则下列结论正确的是( )
如图1所示,一轻弹簧下端固定在水平面上,上端放置一小物体,小物体处于静止状态.现对小物体施一竖直向上的拉力F,使小物体向上做匀加速直线运动,拉力F与物体位移x的关系如图2所示,a、b、c均为已知量,重力加速度为g,弹簧始终在弹性限度内.则下列结论正确的是( )
 如图1所示,一轻弹簧下端固定在水平面上,上端放置一小物体,小物体处于静止状态.现对小物体施一竖直向上的拉力F,使小物体向上做匀加速直线运动,拉力F与物体位移x的关系如图2所示,a、b、c均为已知量,重力加速度为g,弹簧始终在弹性限度内.则下列结论正确的是( )
如图1所示,一轻弹簧下端固定在水平面上,上端放置一小物体,小物体处于静止状态.现对小物体施一竖直向上的拉力F,使小物体向上做匀加速直线运动,拉力F与物体位移x的关系如图2所示,a、b、c均为已知量,重力加速度为g,弹簧始终在弹性限度内.则下列结论正确的是( )| A. | 弹簧的劲度系数为$\frac{b-a}{c}$ | |
| B. | 物体的质量为$\frac{a}{g}$ | |
| C. | 物体的加速度大小为$\frac{a}{b-a}$g | |
| D. | 物体从开始运动到离开弹簧的过程经过的时间为$\sqrt{\frac{2c(b-a)}{ag}}$ |
12.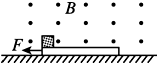 如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
 如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )| A. | 木板和滑块一直做加速度为2m/s2的匀加速运动 | |
| B. | 滑块开始做加速度减小的变加速运动,最后做速度为10 m/s的匀速运动 | |
| C. | 木板先做加速度为2m/s2的匀加速运动,再做加速度增大的运动,最后做加速度为3 m/s2的匀加速运动 | |
| D. | t=3s后滑块和木板有相对运动 |
8. 如图,用恒力F拉着三个物体在光滑的水平面上一起运动.现在中间物体上加上一个小物体,那么连接物体的绳子张力和未放小物体前相比( )
如图,用恒力F拉着三个物体在光滑的水平面上一起运动.现在中间物体上加上一个小物体,那么连接物体的绳子张力和未放小物体前相比( )
 如图,用恒力F拉着三个物体在光滑的水平面上一起运动.现在中间物体上加上一个小物体,那么连接物体的绳子张力和未放小物体前相比( )
如图,用恒力F拉着三个物体在光滑的水平面上一起运动.现在中间物体上加上一个小物体,那么连接物体的绳子张力和未放小物体前相比( )| A. | Ta变小 | B. | Ta变大 | C. | Tb减小 | D. | Tb不变 |
7. 如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )
如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )
 如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )
如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )| A. | $\frac{g}{2}$sinα | B. | 1.5gsinα | C. | gsinα | D. | 2gsinα |
6.质量为m的木块位于粗糙水平面上,若用大小为F的水平恒力拉木块,其加速度为a1,当拉力方向不变,大小变成2F时,木块的加速度为a2,则( )
0 149239 149247 149253 149257 149263 149265 149269 149275 149277 149283 149289 149293 149295 149299 149305 149307 149313 149317 149319 149323 149325 149329 149331 149333 149334 149335 149337 149338 149339 149341 149343 149347 149349 149353 149355 149359 149365 149367 149373 149377 149379 149383 149389 149395 149397 149403 149407 149409 149415 149419 149425 149433 176998
| A. | a2=a1 | B. | a2<a1 | C. | a2=2a1 | D. | a2>2a1 |
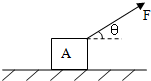 如图,箱子重力为G=220N,在与水平地面成θ=37°角的F=100N的恒定拉力作用下匀速前进,求:
如图,箱子重力为G=220N,在与水平地面成θ=37°角的F=100N的恒定拉力作用下匀速前进,求: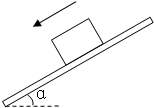 滑块的重力为G=20N,当木板的倾角为α=37°时,滑块恰能匀速下滑.求:
滑块的重力为G=20N,当木板的倾角为α=37°时,滑块恰能匀速下滑.求: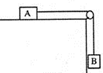 如图所示,物体A放在光滑水平面上(距离右端定滑轮足够远),与物体B用跨过光滑定滑轮的细线相连接,质量分别为mA=1Kg和mB=2Kg.现让它们由静止开始运动,重力加速度为g=10m/s2,求:
如图所示,物体A放在光滑水平面上(距离右端定滑轮足够远),与物体B用跨过光滑定滑轮的细线相连接,质量分别为mA=1Kg和mB=2Kg.现让它们由静止开始运动,重力加速度为g=10m/s2,求: