��Ŀ����
15�� ��ͼ����С�������������ϵı�ֽ���ϣ���ˮƽ���ҵ�������ֽ��Ѹ�ٳ����������ƶ���С������Ǵ����Ϥ�Ĺ�����ʾʵ�飮�������ֽ��������ֱ�ΪM��m�����Ӵ����Ķ�Ħ��������Ϊ�̣�������ֽ����˵ľ��뼰�����Ҷ˵ľ����Ϊd������ˮƽ���ҵĺ㶨����F����ֽ�壬����˵����ȷ���ǣ�������
��ͼ����С�������������ϵı�ֽ���ϣ���ˮƽ���ҵ�������ֽ��Ѹ�ٳ����������ƶ���С������Ǵ����Ϥ�Ĺ�����ʾʵ�飮�������ֽ��������ֱ�ΪM��m�����Ӵ����Ķ�Ħ��������Ϊ�̣�������ֽ����˵ľ��뼰�����Ҷ˵ľ����Ϊd������ˮƽ���ҵĺ㶨����F����ֽ�壬����˵����ȷ���ǣ�������| A�� | ֽ����������˶�ʱ��ֽ������Ħ�����Ĵ�СΪ�̣�M+m��g | |
| B�� | Ҫʹֽ����������˶���Fһ������2�̣�M+m��g | |
| C�� | ��������ֽ�����ʱ���ٶ�С��$\sqrt{��gd}$�����벻��������ϵ��� | |
| D�� | ��F=�̣�2M+4m��gʱ������ǡ�õ��������Ե |
���� Ӧ��Ħ������ʽ���ֽ���������ܵ���Ħ������Ȼ�����Ħ������С������ţ�ٵڶ�����������ٶȣ�Ҫʹֽ������������˶���ֽ��ļ��ٶ�Ӧ��������ļ��ٶȣ�Ȼ�������������Сֵ��
��F=�̣�2M+4m��gʱ������ţ�ٵڶ����ɷ�����������ֽ����ٶȣ�����˶�ѧ��ʽ�������ʱ������ٶȣ�����ٶ�λ�ƹ�ʽ��������ٶȼ�Ϊ���λ�ã��Ӷ��жϳ������λ��
��� �⣺A����ֽ����������˶�ʱ��ֽ�����ܵ�Ħ�������̣�M+m��g+��Mg����A����
B��������ļ��ٶ�Ϊa1��ֽ��ļ��ٶ�Ϊa2�����У���Mg=Ma1��F-��Mg-�̣�M+m��g=ma2����������˶���Ҫa2��a1����ã�F��2�̣�M+m��g����B��ȷ��
C����������ֽ�����ʱ���ٶ�С��$\sqrt{��gd}$�������ȼ����˶���λ��С��$\frac{{v}^{2}}{2a}$=$\frac{d}{2}$���ȼ����˶���λ��С��$\frac{{v}^{2}}{2a��}$=$\frac{��gd}{2��g}$=$\frac{d}{2}$������λ��С��d�������������£���C��ȷ��
D����F=�̣�2M+4m��gʱ������δ����ʱ�ļ��ٶ�a1=��g��ֽ��ļ��ٶȣ�a2=$\frac{F-�̣�M+m��g-��Mg}{m}$=3��g������$\frac{1}{2}$a2t2-$\frac{1}{2}$a1t2=d����ã�t=$\sqrt{\frac{d}{��g}}$�����ʱ������ٶ�v=a1t=$\sqrt{��gd}$����������ֽ������ȼ����˶����ȼ����˶��ļ��ٶȴ�Сa��=��g�����ȼ����˶���λ�ƣ�x=$\frac{{v}^{2}}{2a��}$=$\frac{1}{2}$d�����ȼ����˶���λ��x��=$\frac{1}{2}$a1t2=$\frac{1}{2}$d��������ǡ�õ��������Ե����D��ȷ��
��ѡ��BCD��
���� ���⿼������������С��Ӧ��Ħ������ʽ���Ħ������С��֪������������Ҫ�����������Ӧ��ţ�ٵڶ��������˶�ѧ��ʽ������ȷ���⣮

 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д� �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�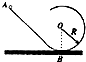 ��ͼ��ʾ���̶���б���¶���뾶ΪR��Բ���ƽ�����ӣ���ʹС���б����ij�ߴ��ɾ�ֹ�ͷţ�����һ��Ħ������ҪʹС����Բ����ϣ��˵���⣩����Բ��������ͷŵĸ߶�hΪ��������
��ͼ��ʾ���̶���б���¶���뾶ΪR��Բ���ƽ�����ӣ���ʹС���б����ij�ߴ��ɾ�ֹ�ͷţ�����һ��Ħ������ҪʹС����Բ����ϣ��˵���⣩����Բ��������ͷŵĸ߶�hΪ��������| A�� | h��2.5R | B�� | h��2R | C�� | h��2.5R��h��R | D�� | 2R��h��2.5R��h��R |
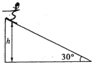 ��ͼ��ʾ��ij�λ�ѩѩ�����Ϊ30�㣬������Ϊm�Ļ�ѩ�˶�Ա�Ӿ�˸�Ϊh����ѩ�����ɾ�ֹ��ʼ�ȼ����»������ٶ�Ϊ$\frac{1}{3}$g�˶�Ա�������»����˵Ĺ����У�������
��ͼ��ʾ��ij�λ�ѩѩ�����Ϊ30�㣬������Ϊm�Ļ�ѩ�˶�Ա�Ӿ�˸�Ϊh����ѩ�����ɾ�ֹ��ʼ�ȼ����»������ٶ�Ϊ$\frac{1}{3}$g�˶�Ա�������»����˵Ĺ����У�������| A�� | ����������Ϊ$\frac{1}{3}$mgh | B�� | ���ӵĶ���Ϊ$\frac{2}{3}$mgh | ||
| C�� | �˷�Ħ��������Ϊ$\frac{1}{3}$mgh | D�� | ���ٵĻ�е��Ϊ$\frac{1}{6}$mgh |
 ��ͼ��ʾ��б�����Ϊ37�㣬����1����б�浲�崦������1��б��䶯Ħ��������=0.5��һ���ܳ��IJ����쳤����������⻬���ʶ�����һ�˹̶���1�ϡ���һ�˹̶�������2�ϣ�����2�¶˹̶�һ��Ϊh�������������¶�˩������3�ϣ�����1��2��3������֮��Ϊ4��1��5����ʼʱ��ס3��3������ĸ߶�Ϊh����ʱ�������պ�������������غ�����gȡ10m/s2������3�Ӿ�ֹͻȻ�ͷź�����1��б���ϻ���������Ϊ��������
��ͼ��ʾ��б�����Ϊ37�㣬����1����б�浲�崦������1��б��䶯Ħ��������=0.5��һ���ܳ��IJ����쳤����������⻬���ʶ�����һ�˹̶���1�ϡ���һ�˹̶�������2�ϣ�����2�¶˹̶�һ��Ϊh�������������¶�˩������3�ϣ�����1��2��3������֮��Ϊ4��1��5����ʼʱ��ס3��3������ĸ߶�Ϊh����ʱ�������պ�������������غ�����gȡ10m/s2������3�Ӿ�ֹͻȻ�ͷź�����1��б���ϻ���������Ϊ��������| A�� | 3h | B�� | $\frac{7}{3}$h | C�� | 2h | D�� | $\frac{4}{3}$h |

| A�� | $\frac{{\sqrt{3}}}{3}{v_0}$ $\frac{1}{2}{v_0}$ | B�� | $\frac{{\sqrt{3}}}{3}{v_0}$ $\frac{{\sqrt{3}}}{3}{v_0}$ | C�� | $\frac{1}{2}{v_0}$ $\frac{{\sqrt{3}}}{3}{v_0}$ | D�� | $\frac{{\sqrt{3}}}{6}{v_0}$ $\frac{{\sqrt{3}}}{3}{v_0}$ |
 �⻬ˮƽ������һ����ΪM=2kg���㹻����ľ�壬ľ���������Ҷ���һ��С�ɺ��ԡ�����Ϊm=3kg����飬�����ľ���Ķ�Ħ��������=0.4�������Ħ�������ڻ���Ħ��������ʼʱ����ľ�嶼��ֹ����ľ�����L=2.4m����һ�̶���ˮƽ���ϵ���ֱ���Ե���P���ֶ����ʩ��һˮƽ��������F=6N����ľ���뵲��P����ײ��ʱ�伫�̣�����ײ��ʱ������ʧ�����ʼ��δ���뵲����ײ����
�⻬ˮƽ������һ����ΪM=2kg���㹻����ľ�壬ľ���������Ҷ���һ��С�ɺ��ԡ�����Ϊm=3kg����飬�����ľ���Ķ�Ħ��������=0.4�������Ħ�������ڻ���Ħ��������ʼʱ����ľ�嶼��ֹ����ľ�����L=2.4m����һ�̶���ˮƽ���ϵ���ֱ���Ե���P���ֶ����ʩ��һˮƽ��������F=6N����ľ���뵲��P����ײ��ʱ�伫�̣�����ײ��ʱ������ʧ�����ʼ��δ���뵲����ײ����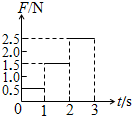
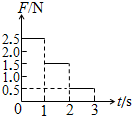

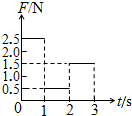
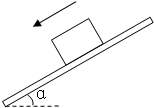 ���������ΪG=20N����ľ������Ϊ��=37��ʱ������ǡ�������»�����
���������ΪG=20N����ľ������Ϊ��=37��ʱ������ǡ�������»�����