10．将两个偏振片紧靠在一起，把它们放在一盏灯前面，没有光通过；若将其中一个偏振片旋转180°，在旋转过程中将会出现（ ）
| A． | 透过偏振片的光的强度先增强，后又减弱到零 | |
| B． | 透过偏振片的光的强度先增强，后又减弱到不为零的最小值 | |
| C． | 透过偏振片的光的强度始终增强 | |
| D． | 透过偏振片的光的强度先增强，后减弱，再增强 |
如图，处于匀强电场中的足够长的绝缘斜面上有一带电滑块，给滑块初动能100J使它从A点出发沿斜面向上运动，第一次运动到斜面上B点时，动能减少了80J，重力势能增加了50J，克服电场力做功20J，则滑块再一次回到B点时的动能为15J．
8．
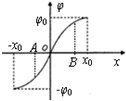某静电场中的一条电场线与x轴重合，其电势的变化规律图象关于O点对称，如图所示．已知x轴上A、B两点中A到O点的距离更近．在O点由静止释放一电子，电子仅受电场力的作用，则下述正确的是（ ）
某静电场中的一条电场线与x轴重合，其电势的变化规律图象关于O点对称，如图所示．已知x轴上A、B两点中A到O点的距离更近．在O点由静止释放一电子，电子仅受电场力的作用，则下述正确的是（ ）| A． | A、B两点的电场强度大小EA＞EB | B． | A、B两点的电场强度方向相反 | ||
| C． | 电子运动的加速度逐渐减小 | D． | 电子将在-x0-+x0之间作往复运动 |
7．
如图所示，Q1Q2为两个固定在绝缘水平面上的异性点电荷，其中Q1为负电荷，Q1的电荷量是Q2的四倍，它们相距L．在其连线上有一点P，P离Q2的距离为$\frac{L}{2}$．下列说法正确的是（ ）
如图所示，Q1Q2为两个固定在绝缘水平面上的异性点电荷，其中Q1为负电荷，Q1的电荷量是Q2的四倍，它们相距L．在其连线上有一点P，P离Q2的距离为$\frac{L}{2}$．下列说法正确的是（ ）| A． | P右侧各点电场强度方向均向右 | |
| B． | 从P右侧到无穷远，各点电场强度依次是先变大后变小 | |
| C． | 从P右侧到无穷远，各点电势依次是先降低再升高 | |
| D． | 负电荷从P点沿两电荷连线向右移到无穷远，其电势能先增大后减小 |
6．
如图所示为等量异性点电荷的电场，矩形abcd的中心正好与两电荷连线的中点o重合，ad边平行于点电荷连线，e、f、g、h分别为矩形各边与两电荷连线及中垂线的交点，取无穷远为零势．下述正确的是（ ）
如图所示为等量异性点电荷的电场，矩形abcd的中心正好与两电荷连线的中点o重合，ad边平行于点电荷连线，e、f、g、h分别为矩形各边与两电荷连线及中垂线的交点，取无穷远为零势．下述正确的是（ ）| A． | ad两点电场强度大小相等，电势相等 | |
| B． | ab两点电场强度相等，电势相等 | |
| C． | ac两点电场强度相等，电势的绝对值相等 | |
| D． | 如果把-Q换成+Q，其它一切不变，则a c两点电场强度等大反向，电势相等 |
5．
如图所示，金属球壳A带有正电，其上方有一小孔a，静电计B的金属球b用导线与金属小球c相连，以下操作所发生的现象正确的是（ ）
如图所示，金属球壳A带有正电，其上方有一小孔a，静电计B的金属球b用导线与金属小球c相连，以下操作所发生的现象正确的是（ ）| A． | 将c移近A，但不与A接触，B会张开一定角度 | |
| B． | 将c与A外表面接触后移开A，B会张开一定角度 | |
| C． | 将c与A内表面接触时，B不会张开角度 | |
| D． | 将c从导线上解下，然后用绝缘细绳吊着从A中小孔置入A内，并与其内壁接触，再提出空腔，与b接触，B会张开一定角度 |
如图所示，一质量为M的楔形木块放在水平桌面上，它的顶角为90°，两底角为α和β；a、b为两个位于斜面上质量均为m的小木块．已知所有接触面都是光滑的．现使a、b同时沿斜面下滑．
2．某实验小组探究弹簧的劲度系数k与其长度（圈数）的关系．实验装置如图（a）所示：一均匀长弹簧竖直悬挂，7个指针P0、P1、P2、P3、P4、P5、P6分别固定在弹簧上距悬点0、10、20、30、40、50、60圈处；通过旁边竖直放置的刻度尺，可以读出指针的位置，P0指向0刻度．设弹簧下端未挂重物时，各指针的位置记为x0；挂有质量为0.100kg的砝码时，各指针的位置记为x．测量结果及部分计算结果如下表所示（n为弹簧的圈数，重力加速度取9.80m/s2）．已知实验所用弹簧总圈数为60，整个弹簧的自由长度为11.88cm．
（1）将表中数据补充完整：①81.7；②0.0122．
（2）以n为横坐标，$\frac{1}{k}$为纵坐标，在图（b）给出的坐标纸上画出$\frac{1}{k}$ n图象．
（3）图（b）中画出的直线可近似认为通过原点．若从实验中所用的弹簧截取圈数为n的一段弹簧，该弹簧的劲度系数k与其圈数n的关系的表达式为k=$\frac{1.67×1{0}^{3}}{n}$N/m．
（1）将表中数据补充完整：①81.7；②0.0122．
| P1 | P2 | P3 | P4 | P5 | P6 | |
| x0（cm） | 2.04 | 4.06 | 6.06 | 8.05 | 10.03 | 12.01 |
| x（cm） | 2.64 | 5.26 | 7.81 | 10.30 | 12.93 | 15.41 |
| n | 10 | 20 | 30 | 40 | 50 | 60 |
| k（N/m） | 163 | ① | 56.0 | 43.6 | 33.8 | 28.8 |
| $\frac{1}{k}$（m/N） | 0.0061 | ② | 0.0179 | 0.0229 | 0.0296 | 0.0347 |
（3）图（b）中画出的直线可近似认为通过原点．若从实验中所用的弹簧截取圈数为n的一段弹簧，该弹簧的劲度系数k与其圈数n的关系的表达式为k=$\frac{1.67×1{0}^{3}}{n}$N/m．
1．
位于坐标原点O的质点在F1、F2和F3三力的作用下保持静止，已知其中F1的大小恒定不变，方向沿y轴负方向的；F2的方向与x轴正方向的夹角为θ（θ＜45°），但大小未知，如图所示，则下列关于力F3的判断正确的是（ ）
0 145031 145039 145045 145049 145055 145057 145061 145067 145069 145075 145081 145085 145087 145091 145097 145099 145105 145109 145111 145115 145117 145121 145123 145125 145126 145127 145129 145130 145131 145133 145135 145139 145141 145145 145147 145151 145157 145159 145165 145169 145171 145175 145181 145187 145189 145195 145199 145201 145207 145211 145217 145225 176998
位于坐标原点O的质点在F1、F2和F3三力的作用下保持静止，已知其中F1的大小恒定不变，方向沿y轴负方向的；F2的方向与x轴正方向的夹角为θ（θ＜45°），但大小未知，如图所示，则下列关于力F3的判断正确的是（ ）| A． | F3的最小值为F1cosθ | B． | F3的大小可能为F1sinθ | ||
| C． | 力F3可能在第三象限 | D． | F3与F2的合力大小与F2的大小有关 |