题目内容
如图所示，质量M=1.5 kg的小车静止于光滑水平面上并靠近固定在水平面上的桌子右边，其上表面与水平桌面相平，小车的左端放有一质量为0.5 kg的滑块Q。水平放置的轻弹簧左端固定，质量为0.5 kg的小物块P置于桌面上的A点并与弹簧的右端接触，此时弹簧处于原长。现用水平向左的推力将P缓慢推至B点（弹簧仍在弹性限度内）时，推力做的功为WF=4 J，撤去推力后，P沿光滑的桌面滑到小车左端并与Q发生弹性碰撞，最后Q恰好没从小车上滑下。已知Q与小车表面间动摩擦因数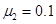
。（g=10
m/s2）
（1）Q刚在小车上滑行时的初速度v0 ；
（2）小车的长度至少为多少才能保证滑块Q不掉下？
【答案】
（1）
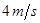（2）6m
【解析】
试题分析：（1）用水平向左的推力缓慢压缩弹簧，弹簧获得的弹性势能等于推力做的功．即：弹簧的弹性势能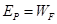
．
当弹簧完全推开物块P时弹簧的弹性势能转化为物块P的动能，有：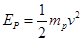
解得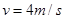
，
P、Q之间发生弹性碰撞时，动量守恒，机械能也守恒，于是有：
，
，
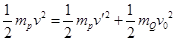（2分）
根据以上两式解得：
（1分）
（2）滑块Q在小车上滑行，做匀减速运动，根据牛顿第二定律得
解得：
小车开始做初速度为零的匀加速运动，根据牛顿第二定律得
解得：
小车和滑块达到相等速度时不掉下来就不会掉下来，此过程滑块Q相对小车滑行的位移大小等于车子的最小长度L．设两者达到共同速度的时间为t，根据运动学公式有：
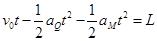解得：
解得：
故小车的最小长度为6m．
考点：本题考查考生对功能关系、动量守恒定律、机械能守恒定律、牛顿第二定律的理解和应用．意在考查考生应用动量观点和能量观点解决碰撞问题的能力．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
如图所示，质量M=1.0kg的木块随传送带一起以v=2.0m/s的速度向左匀速运动，木块与传送带间的动摩擦因数μ=0.50．当木块运动至最左端A点时，一颗质量m=20g的子弹以v0=3.0×102m/s水平向右的速度击穿木块，穿出木块时的速度v1=50m/s．设传送带的速度始终恒定，子弹击穿木块的时间极短，且不计木块质量变化，g=10m/s2．求：
如图所示，质量m=1.0kg的小球B静止在平台上，平台高h=0.8m．一个质量M=2.0kg的小球A沿平台自左向右运动，与小球B处发生正碰，碰后小球B的速度vB=6.0m/s，小球A落在水平地面的C点，DC间距离s=1.2m．求：
如图所示，质量m=1.0kg的物体静止水平面上，水平恒力F=3.0作用于物体上，使物体从静止开始运动，经时间t=2.0s撤去拉力F，已知物体与水平面间的动摩擦因数μ=0.15，取g=10m/s2．求：
如图所示，质量M=1.0kg，长L=l．0m的木板静止在粗糙的水平地面上，木板与地面间的动摩擦因数μ1=0.1kg．在木板的左端放置一个质量m=1.0kg、大小可以忽略的铁块，铁块与木板间的动摩擦因数μ2=0.4．认为最大静摩擦力等于滑动摩擦力，取g=10m/s2．若在铁块上加一个水平向右的恒力F=8.0N，求：