题目内容
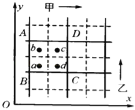
【题目】如图，两平行金属板水平放置，板长为L，间距为d，板间电压为U，一个不计重力的电荷量为q的带电粒子以初速度v0沿两板的中线射入，恰好沿下板的边缘飞出，粒子通过平行金属板的时间为t，则（ ）
A. 在
时间内，电场力对粒子做的功为
B. 在时间内，电场力对粒子做的功为
C. 在粒子下落的前
和后过程中，电场力做功之比为1:2
D. 在粒子下落的前和后过程中，电场力做功之比为1:1
【答案】D
【解析】
试题设粒子在前
时间内和在后时间内竖直位移分别为y1、y2，由y=
at2和匀变速直线运动的推论可知y1：y2=1：3，得：y1=
d，y2=
d，则在前时间内，电场力对粒子做的功为：W1=qU=qU，
在后时间内，电场力对粒子做的功为：W2=qU=qU．故AB错误；根据W=qEy可得，在粒子下落前
和后的过程中，电场力做功之比为1：1，故C错误，D正确；故选D．
名校课堂系列答案
【题目】（8分）利用气垫导轨验证机械能守恒定律。实验装置示意图如图1所示，实验步骤：
A．将气垫导轨放在水平桌面上，桌面高度不低于1m，将导轨调至水平。 |
B．用游标卡尺测量挡光条的宽度d |
C．由导轨标尺读出两光电门中心之间的距离s |
D．将滑块移至光电门1左侧某处，待砝码静止不动时，释放滑块，要求砝码落地前挡光条已通过光电门2。 |
E．从数字计时器（图1中未画出）上分别读出挡光条通过光电门1和光电门2所用的时间Δt1和Δt2。
F．用天平称出滑块和挡光条的总质量M，再称出托盘和砝码的总质量m。
用表示直接测量量的字母写出下列所求物理量的表达式：
（1）滑块通过光电门1和光电门2时的瞬时速度分别为v1= 和v2=
（2）在滑块从光电门1运动到光电门2的过程中，系统势能的减少量ΔEp=____ __（重力加速度为g）。系统（包括滑块，挡光条、托盘和砝码）动能的增加量ΔEk=__ ____
（3）如果ΔEp=ΔEk，则可认为验证了机械能守恒定律。
