题目内容
弹性小球从某一高度H自由下落到水平地面上,与水平地面碰撞后弹起,假设小球与地面的碰撞过程中没有能量损失,但由于受到大小不变的空气阻力的影响,使每次碰撞后弹起上升的高度是碰撞前下落高度的
.为使小球弹起后能上升到原来的高度H,则需在小球开始下落时,在极短时间内给它一个多大的初速度v0?
某同学对此解法是:由于只能上升
H,所以机械能的损失为
mgH,只要补偿损失的机械能即可回到原来的高度,因此
mv02=
mgH,得v0=
H.
你同意上述解法吗?若不同意,请简述理由并求出你认为正确的结果.
| 3 |
| 4 |
某同学对此解法是:由于只能上升
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
|
你同意上述解法吗?若不同意,请简述理由并求出你认为正确的结果.
不同意,该学生只考虑小球回到
H后要继续上升所需克服重力做功的动能,忽略了继续上升时还要有能量克服空气阻力做功.
正确的解法是:
根据动能定理得:WG+Wf=△Ek
对第一种情况的整个过程:
mgH-
fH=0
得空气阻力大小为:f=
mg
对第二情况:Wf=0-
m
即:-2fH=0-
m
则得:
mg2H=
m
解得:v0=
答:不同意,该学生只考虑小球回到
H后要继续上升所需克服重力做功的动能,忽略了继续上升时还要有能量克服空气阻力做功.正确的结果是:初速度v0为
.
| 3 |
| 4 |
正确的解法是:
根据动能定理得:WG+Wf=△Ek
对第一种情况的整个过程:
| 1 |
| 4 |
| 7 |
| 4 |
得空气阻力大小为:f=
| 1 |
| 7 |
对第二情况:Wf=0-
| 1 |
| 2 |
| v | 20 |
即:-2fH=0-
| 1 |
| 2 |
| v | 20 |
则得:
| 1 |
| 7 |
| 1 |
| 2 |
| v | 20 |
解得:v0=
|
答:不同意,该学生只考虑小球回到
| 3 |
| 4 |
|

练习册系列答案
相关题目

 .为使小球弹起后能上升到原来的高度H,则需在小球开始下落时,在极短时间内给它一个多大的初速度v?
.为使小球弹起后能上升到原来的高度H,则需在小球开始下落时,在极短时间内给它一个多大的初速度v? H,所以机械能的损失为
H,所以机械能的损失为 mgH,只要补偿损失的机械能即可回到原来的高度,因此
mgH,只要补偿损失的机械能即可回到原来的高度,因此 mv2=
mv2= mgH,得v=
mgH,得v=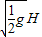 .
.