题目内容
(1)弹性小球从某一高度H下落到水平地面上,与水平地面碰撞后弹起,假设小球与地面的碰撞过程中没有能量损失,但由于受到大小不变的空气阻力的影响,使每次碰撞后弹起上升的高度是碰撞前下落高度的3/4.机械能损失
.为使小球弹起后能上升到原来的高度H,则需在小球开始下落时,在极短时间内给它一个多大的初速度vo=
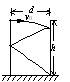
(2)如图的游标卡尺的示数为(a)

图a.
| mgH |
| 4 |
| mgH |
| 4 |
2
|
2
,才能弹回到原来的高度H.
|
(2)如图的游标卡尺的示数为(a)
10.03cm
10.03cm
cm,(b)1.09cm
1.09cm
cm.
图a.
分析:(1)根据能量守恒,抓住小球机械能的减小量求出机械能的损失.小球下落过程中,重力做正功,空气阻力做负功,对由静止释放和有初速度释放分别运用动能定理研究列式,即可求出小球应需多大的初速度.
(2)游标卡尺的读数等于主尺读数加上游标读数,不需估读.
(2)游标卡尺的读数等于主尺读数加上游标读数,不需估读.
解答:解:(1)规定地面为零势能平面,小球开始下落时的机械能为mgH,反弹到最大高度时机械能为
mgH,知在此过程机械能的损失为
.
设空气阻力大小为f,则:
当物体由静止释放时,全过程运用动能定理得,mg?
-f?
=0
当物体有初速度时,全过程运用动能定理得,-f?2H=0-
mv02
联立两式解得v0=2
.
(2)图a的游标卡尺的精确度为0.1mm,则读数为100mm+0.1×3mm=100.3mm=10.03cm.
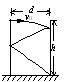
图b的游标卡尺的精确度为0.1mm,则读数为10mm+0.1×9mm=10.9mm=1.09cm.
故答案为:(1)
,2
(2)10.03,1.09
| 3 |
| 4 |
| mgH |
| 4 |
设空气阻力大小为f,则:
当物体由静止释放时,全过程运用动能定理得,mg?
| H |
| 4 |
| 7H |
| 4 |
当物体有初速度时,全过程运用动能定理得,-f?2H=0-
| 1 |
| 2 |
联立两式解得v0=2
|
(2)图a的游标卡尺的精确度为0.1mm,则读数为100mm+0.1×3mm=100.3mm=10.03cm.
图b的游标卡尺的精确度为0.1mm,则读数为10mm+0.1×9mm=10.9mm=1.09cm.
故答案为:(1)
| mgH |
| 4 |
|
点评:本题考查动能定理的运用以及游标卡尺的读数,难度中等,对于动能定理解题,关键选择合适的研究过程,根据动能定理列式求解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
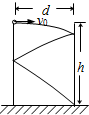 两个竖直放置的钢板平行地固定在水平面上,钢板高度为h=1.25m,相距d=0.90m.将一个弹性小球从左面钢板的最上端处以某一初速度正对着右面的钢板平抛出去,小球依次在两个钢板上各碰撞一次后,恰好落在右面钢板的底端.小球和钢板的碰撞过程中没有能量损失.求:小球平抛的初速度大小v0.
两个竖直放置的钢板平行地固定在水平面上,钢板高度为h=1.25m,相距d=0.90m.将一个弹性小球从左面钢板的最上端处以某一初速度正对着右面的钢板平抛出去,小球依次在两个钢板上各碰撞一次后,恰好落在右面钢板的底端.小球和钢板的碰撞过程中没有能量损失.求:小球平抛的初速度大小v0.