题目内容
14.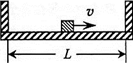 如图所示,质量为M,内壁间距为L的箱子静止于光滑的水平面上,在箱子正中间放着一质量为m的小物块(可视为质点).现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,并与箱子保持相对静止.已知小物块与箱子发生的碰撞均为弹性碰撞,重力加速度为g,求小物块与箱子底板间的动摩擦因数μ.
如图所示,质量为M,内壁间距为L的箱子静止于光滑的水平面上,在箱子正中间放着一质量为m的小物块(可视为质点).现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,并与箱子保持相对静止.已知小物块与箱子发生的碰撞均为弹性碰撞,重力加速度为g,求小物块与箱子底板间的动摩擦因数μ.
分析 根据动量守恒求得系统最终速度,再根据能量守恒求得动摩擦因数.
解答 解:小物块与箱子发生N次碰撞恰好又回到箱子正中间,由此可知,小物块相对于箱子滑动的距离S=NL.
根据动量守恒条件可知,小物块与箱子组成的系统水平方向动量守恒,可知,令共同速度为v′,则有:
mv=(M+m)v′
可得系统共同速度为:v$′=\frac{m}{m+M}v$
小物块受到摩擦力为:f=μmg
根据能量守恒定律有:$\frac{1}{2}m{v}^{2}=\frac{1}{2}(M+m)v{′}^{2}+fS$
可得动摩擦因数:$μ=\frac{\frac{1}{2}m{v}^{2}-\frac{1}{2}(M+m)v{′}^{2}}{mgS}$=$\frac{M{v}^{2}}{2N(M+m)gL}$
答:小物块与箱子底板间的动摩擦因数μ为$\frac{M{v}^{2}}{2N(M+m)gL}$.
点评 解决本题的关键是能抓住系统动量守恒和能量守恒确定摩擦力情况,知道系统损失的机械能等于物块所受摩擦力从而求得动摩擦因数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 按照我国月球探测活动计划,在第一步“绕月”工程圆满完成任务后,将开展第二步“落月”工程,预计在2013年前完成.假设月球半径为R,月球表面的重力加速度为g0.飞船沿距月球表面高度为3R的圆形轨道I运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.下列判断正确的是( )
按照我国月球探测活动计划,在第一步“绕月”工程圆满完成任务后,将开展第二步“落月”工程,预计在2013年前完成.假设月球半径为R,月球表面的重力加速度为g0.飞船沿距月球表面高度为3R的圆形轨道I运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.下列判断正确的是( )
 按照我国月球探测活动计划,在第一步“绕月”工程圆满完成任务后,将开展第二步“落月”工程,预计在2013年前完成.假设月球半径为R,月球表面的重力加速度为g0.飞船沿距月球表面高度为3R的圆形轨道I运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.下列判断正确的是( )
按照我国月球探测活动计划,在第一步“绕月”工程圆满完成任务后,将开展第二步“落月”工程,预计在2013年前完成.假设月球半径为R,月球表面的重力加速度为g0.飞船沿距月球表面高度为3R的圆形轨道I运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.下列判断正确的是( )| A. | 飞船在轨道I上的运行速率v=$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在A点点火变轨的瞬间,动能增加 | |
| C. | 飞船在A点的线速度大于在B点的线速度 | |
| D. | 飞船在轨道Ⅲ绕月球运动一周所需的时间为2π$\sqrt{\frac{R}{{g}_{0}}}$ |
5.为了安全,汽车在行驶途中,车与车之间必须保持一定的距离,这是因为从驾驶员看见某一情况到采取制动动作的反应时间里,汽车仍然要通过一段距离,这个距离称为反应距离,而从采取制动动作到汽车停止运动通过的距离称为制动距离.表中是在不同速度下的反应距离和制动距离的部分数据,根据分析计算,表中未给出的数据X应是( )
| 速度m/s | 反应距离m | 制动距离m |
| 15 | 18 | 45 |
| 20 | X | 80 |
| 25 | 30 | 125 |
| A. | X=20 | B. | X=22 | C. | X=24 | D. | X=26 |
19. 如图所示,质量为m的球,被长为L的细绳吊起处于静止状态,现对小球施水平方右的恒力F,小球向右运动到能达到的最高位置时,细绳与竖直立方向的夹角为60°,则恒力F的大小为( )
如图所示,质量为m的球,被长为L的细绳吊起处于静止状态,现对小球施水平方右的恒力F,小球向右运动到能达到的最高位置时,细绳与竖直立方向的夹角为60°,则恒力F的大小为( )
 如图所示,质量为m的球,被长为L的细绳吊起处于静止状态,现对小球施水平方右的恒力F,小球向右运动到能达到的最高位置时,细绳与竖直立方向的夹角为60°,则恒力F的大小为( )
如图所示,质量为m的球,被长为L的细绳吊起处于静止状态,现对小球施水平方右的恒力F,小球向右运动到能达到的最高位置时,细绳与竖直立方向的夹角为60°,则恒力F的大小为( )| A. | $\frac{1}{2}$mg | B. | $\frac{\sqrt{3}}{3}$mg | C. | $\frac{\sqrt{3}}{2}$mg | D. | $\sqrt{3}$mg |
6. 如图所示,一理想变压器原线圈接入一交流电源,副线圈电路中R1、R2、R3和R4均为定值电阻,开关S是断开的,V1.V2为理想电压表,读数分别为U1和U2;Al、A2和A3为理想电流表,读数分别为I1、I2和I3.现闭合S,如果保持U1数值不变,下列推断中正确的是( )
如图所示,一理想变压器原线圈接入一交流电源,副线圈电路中R1、R2、R3和R4均为定值电阻,开关S是断开的,V1.V2为理想电压表,读数分别为U1和U2;Al、A2和A3为理想电流表,读数分别为I1、I2和I3.现闭合S,如果保持U1数值不变,下列推断中正确的是( )
 如图所示,一理想变压器原线圈接入一交流电源,副线圈电路中R1、R2、R3和R4均为定值电阻,开关S是断开的,V1.V2为理想电压表,读数分别为U1和U2;Al、A2和A3为理想电流表,读数分别为I1、I2和I3.现闭合S,如果保持U1数值不变,下列推断中正确的是( )
如图所示,一理想变压器原线圈接入一交流电源,副线圈电路中R1、R2、R3和R4均为定值电阻,开关S是断开的,V1.V2为理想电压表,读数分别为U1和U2;Al、A2和A3为理想电流表,读数分别为I1、I2和I3.现闭合S,如果保持U1数值不变,下列推断中正确的是( )| A. | U2变小、I3变小 | B. | U2不变、I2变大 | C. | I1变大、I2变大 | D. | I1变大、I3变大 |
3. 如图所示,实线为一列正弦波在某一时刻的波形曲线,经过△t=0.7s,其波形如图中虚线所示,T<△t<2T.下列说法正确的是( )
如图所示,实线为一列正弦波在某一时刻的波形曲线,经过△t=0.7s,其波形如图中虚线所示,T<△t<2T.下列说法正确的是( )
 如图所示,实线为一列正弦波在某一时刻的波形曲线,经过△t=0.7s,其波形如图中虚线所示,T<△t<2T.下列说法正确的是( )
如图所示,实线为一列正弦波在某一时刻的波形曲线,经过△t=0.7s,其波形如图中虚线所示,T<△t<2T.下列说法正确的是( )| A. | 波一定向右传播 | |
| B. | 波速和周期可能为0.5m/s和0.56s | |
| C. | 波速和周期可能为0.7m/s和0.40s | |
| D. | 该波遇到大小为0.2m的障碍物,可以发生明显衍射 | |
| E. | 观察者以某一速度向波源靠近时,接收到的频率可能为1.5 Hz |
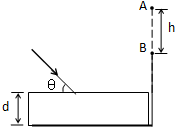 如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.保留两位有效数字.试求:
如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.保留两位有效数字.试求: 甲、乙两物体同时、同向出发,两物体运动的速度图象如图,甲先加速后减速,乙一直匀速,出发时甲在乙的前方,x=1.5m处,两物体相遇而不相碰,求:
甲、乙两物体同时、同向出发,两物体运动的速度图象如图,甲先加速后减速,乙一直匀速,出发时甲在乙的前方,x=1.5m处,两物体相遇而不相碰,求: 如图所示,倾角θ=30°、宽为L=1m的足够长的U形光滑金属导轨固定在磁感应强度B=1T、范围足够大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行于导轨的F牵引一根质量m=0.2kg、电阻R=1Ω的导体棒ab由静止开始沿导轨向上滑动;牵引力的功率恒定为P=90W,经过t=2s导体棒刚达到稳定速度v时棒上滑的距离s=11.9m.导体棒ab始终垂直导轨且与导轨接触良好,不计导轨电阻及一切摩擦,取g=10m/s2.求:
如图所示,倾角θ=30°、宽为L=1m的足够长的U形光滑金属导轨固定在磁感应强度B=1T、范围足够大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行于导轨的F牵引一根质量m=0.2kg、电阻R=1Ω的导体棒ab由静止开始沿导轨向上滑动;牵引力的功率恒定为P=90W,经过t=2s导体棒刚达到稳定速度v时棒上滑的距离s=11.9m.导体棒ab始终垂直导轨且与导轨接触良好,不计导轨电阻及一切摩擦,取g=10m/s2.求: