题目内容
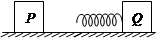
如图所示,质量均为m的小滑块P和Q都视作质点,与轻质弹簧相连的Q静止在光滑水平面上。P以某一初速度v0向Q运动并与弹簧发生碰撞,在整个过程中,弹簧具有的最大弹性势能等于多少?P最终的运动速度为多少?

速度为0
P和Q两者碰撞过程中动量守恒,当两者具有相同速度时,弹簧压缩最多时,弹簧具有最大的弹性势能
m v0=2 m v ① (2分)
Epm=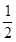 m v02-
m v02-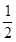 ×2m v2 =
×2m v2 =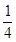 m v02 ② (2分)
m v02 ② (2分)
P和Q两者弹簧压缩后,当弹簧恢复原长,两者分离时,P 的速度最小,
m v0=m v1 +m v2 (2分)
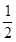 m v02=
m v02=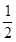 m v12 +
m v12 +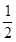 m v22 (2分)
m v22 (2分)
解得v1=0,v2=v0 (1分)
P最终的运动速度为0 .
本题考查动量守恒定律和能量关系,当两物体速度相等时弹性势能最大,弹性势能等于系统动能的减小量
m v0=2 m v ① (2分)
Epm=
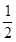 m v02-
m v02-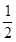 ×2m v2 =
×2m v2 =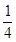 m v02 ② (2分)
m v02 ② (2分)P和Q两者弹簧压缩后,当弹簧恢复原长,两者分离时,P 的速度最小,
m v0=m v1 +m v2 (2分)
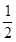 m v02=
m v02=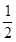 m v12 +
m v12 +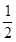 m v22 (2分)
m v22 (2分)解得v1=0,v2=v0 (1分)
P最终的运动速度为0 .
本题考查动量守恒定律和能量关系,当两物体速度相等时弹性势能最大,弹性势能等于系统动能的减小量

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目


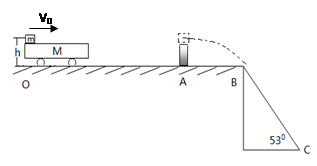
 的小车在光滑的水平面上以速度
的小车在光滑的水平面上以速度 向右做匀速直线运动,一个质量为
向右做匀速直线运动,一个质量为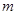 的小球从高
的小球从高 处自由下落,与小车碰撞后反弹上升的高度为仍为
处自由下落,与小车碰撞后反弹上升的高度为仍为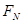 ?
?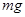 ,小球与车之间的动摩擦因数为
,小球与车之间的动摩擦因数为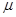 ,则小球弹起时的水平速度可能是
,则小球弹起时的水平速度可能是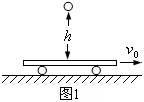
 .
. .
.
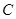 .
.
 .
.
 是否相等,以验证动量守恒。
是否相等,以验证动量守恒。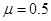 ,斜面的倾角为53°(
,斜面的倾角为53°(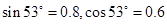 ,g=10m/s2)
,g=10m/s2)