题目内容
如图所示,一位质量m=65kg参加“挑战极限运动”的业余选手,要越过一宽度为s=3m的水沟,跃上高为h=1.8m的平台,采用的方法是:人手握一根长L=3.25m的轻质弹性杆一端。从A点由静止开始匀加速助跑,至B点时,杆另一端抵在O点的阻挡物上,接着杆发生形变。同时人蹬地后被弹起,到达最高点时杆处于竖直,人的重心恰位于杆的顶端,此刻人放开杆水平飞出,最终趴落到平台上,运动过程中空气阻力可忽略不计。(g取10m/s2)
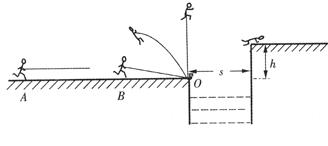
小题1:设人到达B点时速度vB=8m/s,人匀加速运动的加速度a=2m/s2,求助跑距离SAB。
小题2:人要到达平台,在最高点飞出时刻速度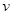 至少多大?
至少多大?
小题3:设人跑动过程中重心离地高度H=1.0m,在(1)、(2)问的条件下,在B点人蹬地弹起瞬间,人至少再做多少功?

小题1:设人到达B点时速度vB=8m/s,人匀加速运动的加速度a=2m/s2,求助跑距离SAB。
小题2:人要到达平台,在最高点飞出时刻速度
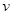 至少多大?
至少多大?小题3:设人跑动过程中重心离地高度H=1.0m,在(1)、(2)问的条件下,在B点人蹬地弹起瞬间,人至少再做多少功?
小题1:
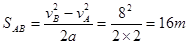
小题2:
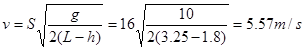
小题3:
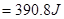
(1)由 (2分)
(2分)
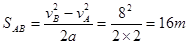 (2分)
(2分)
(2)人飞出作平抛运动,在最高点最小速度为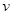 时恰好落在平台上。
时恰好落在平台上。
水平: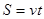 (1分)
(1分)
竖直: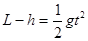 (2分)
(2分)
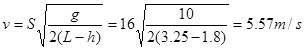 (2分)
(2分)
(3)人蹬地瞬间做功为W
 (3分)
(3分)
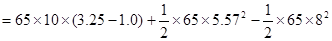
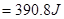 (2分)
(2分)
 (2分)
(2分)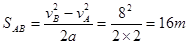 (2分)
(2分)(2)人飞出作平抛运动,在最高点最小速度为
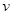 时恰好落在平台上。
时恰好落在平台上。水平:
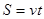 (1分)
(1分)竖直:
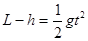 (2分)
(2分)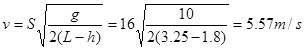 (2分)
(2分)(3)人蹬地瞬间做功为W
 (3分)
(3分)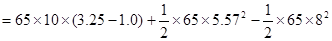
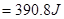 (2分)
(2分)
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
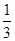 g的加速度减速上升h高度,不计空气阻力,则下列说法中正确的有( )
g的加速度减速上升h高度,不计空气阻力,则下列说法中正确的有( )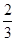 mgh
mgh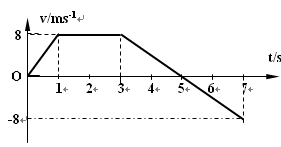
 ,摩擦力做功为
,摩擦力做功为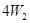
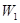 ,摩擦力做功为4
,摩擦力做功为4
 ,摩擦力做功为
,摩擦力做功为

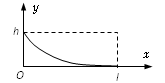

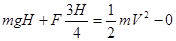 ,解方程得到V的大小。
,解方程得到V的大小。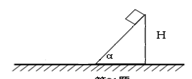
 L,细绳的拉力达到9mg时就会断裂.逐渐增大球的速度,当球某次运动到最低点时绳断裂,忽略手的运动半径和空气阻力,求:
L,细绳的拉力达到9mg时就会断裂.逐渐增大球的速度,当球某次运动到最低点时绳断裂,忽略手的运动半径和空气阻力,求:
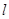 的细绳吊起处于静止状态,质量为m的A球沿半径为
的细绳吊起处于静止状态,质量为m的A球沿半径为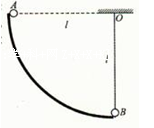
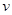 的大小;
的大小;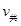 共的大小;
共的大小;