��Ŀ����
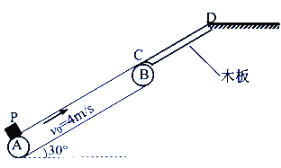
����Ŀ��ij������������Ĵ���ϵͳ�����Ϊ30���Ĵ��ʹ�AB��һ�����ͬ�ij�ľ��CD��ɣ�����ʹ��ʹ���Ķ�Ħ������![]() ����ľ��Ķ�Ħ������
����ľ��Ķ�Ħ������![]() �����ʹ���
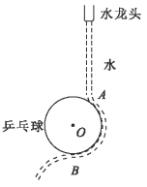
�����ʹ���![]() �ĺ㶨�ٶ�˳ʱ��ת�����ֽ����P�������ڴ��ʹ�A�㣬���ֵ��������B��ʱ�պ���Դ��ʹ���ֹ������D��ʱ�ٶ�ǡ��Ϊ���漴����е��ȡ�ߡ�������Կ����ʵ㣬Ƥ����ľ������Ϊ�����ӣ��������ٶ�g=10m/s2����
�ĺ㶨�ٶ�˳ʱ��ת�����ֽ����P�������ڴ��ʹ�A�㣬���ֵ��������B��ʱ�պ���Դ��ʹ���ֹ������D��ʱ�ٶ�ǡ��Ϊ���漴����е��ȡ�ߡ�������Կ����ʵ㣬Ƥ����ľ������Ϊ�����ӣ��������ٶ�g=10m/s2����
��1�����ʹ��ij���L1��
��2��ľ��ij���L2�Լ������A��D�����ʱ��T��
��3�������е��δ����D�㼰ʱ�����ȡ�ߣ�������������»�����˺�������ľ�����˶�����·��S�Ƕ��٣�
���𰸡���1��3.2m����2��![]() s����3��
s����3��![]()
��������
��1��P����Ƥ����������ͼһ
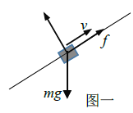
��ţ�ٵڶ�������
![]()
�����ٶ�λ�ƹ�ʽ��
![]()
�����������ݽ��![]()
��2������ľ����C���������ͼ��
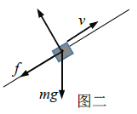
��ţ�ٵڶ����ɵ�
![]()
��C��D����루�峤��Ϊ
![]()
���![]()
��Ƥ�����ϻ�ʱ��Ϊ
![]()
��ľ�����ϻ�ʱ��Ϊ
![]()
������
![]()
��3����D�������˶���������ͼ��

��ţ�ٵڶ����ɵ�
![]()
��һ�η���Bʱ��
![]()
![]()
����B�����Ƥ���������¼��ٺ�����ͬ���ٶȷ��أ����ϳ��λ��
![]()
�ڶ��η���B
![]()
���ϳ�
![]()
���i�����Ͼ���B��ʱ�ٶ�Ϊvi�������ϳ�xi����B��ʱ�ٶ�Ϊ
![]()
��֪��i+1�����Ͼ���B��ʱ�ٶȴ�С��Ϊvi+1���������ϳ��λ��Ϊ
![]()
�����ÿ�γ���ľ��ľ�������һ�ε�![]() �����ɵô˺���黹���ڰ����˶���·��Ϊ
�����ɵô˺���黹���ڰ����˶���·��Ϊ
![]()