题目内容
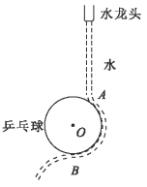
【题目】如图所示，打开水龙头，流出涓涓细流。将乒乓球靠近竖直的水流时，水流会被吸引，顺着乒乓球表面流动。这个现象称为康达效应（Coanda Effect）。某次实验，水流从
点开始顺着乒乓球表面流动，并在乒乓球的最低点
与之分离，最后落在水平地面上的
点（未画出）。已知水流出水龙头的初速度为
，点到点的水平射程为
，点距地面的高度为
，乒乓球的半径为
，
为乒乓球的球心，
与竖直方向的夹角
，不计一切阻力，若水与球接触瞬间速率不变，重力加速度为
。
(1)若质量为
的水受到乒乓球的“吸附力”为
，求
的最大值；
(2)求水龙头下端到的高度差
。
【答案】(1)
；(2)
【解析】
(1)设水流在
点的速率为
，在点时
最大，由牛顿第二定律
①
水流从点开始做平抛运动，有
②
③
联立，解得
④
(2)水流从水龙头流出至到达点，由动能定理
⑤
联立，解得
⑥
练习册系列答案
相关题目
