Question

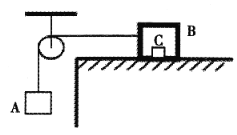
【题目】如图所示，在光滑的水平面上有一足够长的质量为M＝4 kg的长木板，在长木板右端有一质量为m＝1 kg的小物块，长木板与小物块间动摩擦因数为μ＝0.2，长木板与小物块均静止．现用F＝18N的水平恒力向右拉长木板，经时间t＝1s撤去水平恒力F

(1)在F的作用下，长木板的加速度为多大？

(2)刚撤去F时，小物块离长木板右端多远？

(3) 小物块最终离长木板右端多远？

Answer 1

【答案】(1) 4 m/s2(2) 1m(3) 1.8m

【解析】

(1)对木板应用牛顿第二定律可得木板加速度

a1＝

解得

a1＝4m/s2

(2)撤去F之前，小物块只受摩擦力作用，故小物块加速度：

a2＝μg＝2m/s2

小物块相对木板向左的位移

Δx1＝a1t2－a2t2

解得

Δx1＝1m

(3)刚撤去F时，木板的速度：

v1＝a1t＝4m/s

小物块速度

v2＝a2t＝2m/s

撤去F后，长木板的加速度：

a1′＝-＝-0.5m/s2

最终速度

v＝v2＋a2t′＝v1＋a1′t′

解得

t′=0.8s，v＝3.6m/s

在t′内，小物块相对木板向左的位移

Δx2＝－

解得

Δx2＝0.8m

最终小物块离长木板右端

x＝Δx1＋Δx2＝1.8m