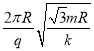题目内容
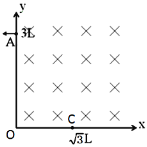
【题目】如图所示,在xoy平面的第Ⅰ象限内存在垂直xoy平面向里的匀强磁场,两个相同的带正电粒子以相同的速率从x轴上坐标(![]() ,0)的C点沿不同方向射入磁场,分别到达y轴上坐标为(0,3L)的A点和B点(坐标未知),到达时速度方向均垂直y轴,不计粒子重力及其相互作用。根据题设条件下列说法正确的是( )
,0)的C点沿不同方向射入磁场,分别到达y轴上坐标为(0,3L)的A点和B点(坐标未知),到达时速度方向均垂直y轴,不计粒子重力及其相互作用。根据题设条件下列说法正确的是( )
A.可以确定带电粒子在磁场中运动的半径
B.若磁感应强度B已知可以求出带电粒子的比荷
C.因磁感应强度B未知故无法求出带电粒子在磁场中运动时间之比
D.可以确定B点的位置坐标
【答案】AD
【解析】
A.已知粒子的入射点及出射方向,同时已知圆上的两点,根据出射点速度相互垂直的方向及AC连线的中垂线的交点即可明确粒子运动圆的圆心位置,由几何关系可知AC长为
![]()
且有
![]()
则
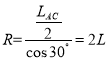
因两粒子的速率相同,且是同种粒子,则可知,它们的半径相同,即两粒子的半径均可求出,故A正确;
B.由公式
![]()
得
![]()
由于不知道粒子的运动速率,则无法求出带电粒子的比荷,故B错误;
C.根据几何关系可知从A射出的粒子对应的圆心角为![]() ,B对应的圆心角为
,B对应的圆心角为![]() ;即可确定对应的圆心角,由公式
;即可确定对应的圆心角,由公式
![]()
由于两粒子是同种粒子,则周期相同,所以可以求出带电粒子在磁场中运动时间之比,故C错误;
D.由几何关系可求得B点对应的坐标,故D正确。
故选AD。
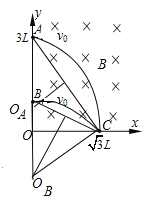

练习册系列答案
相关题目