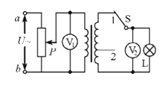
题目内容
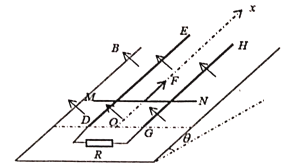
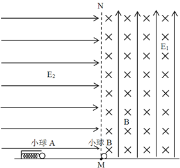
【题目】如图所示,在光滑水平面上距离竖直线MN左侧较远处用弹簧锁定不带电绝缘小球A,弹性势能为0.45J,A球质量M=0.1kg,解除锁定后与静止在M点处的小球B发生弹性正碰,B球质量m=0.2kg、带电量q=+10C。MN左侧存在水平向右的匀强电场E2,MN右侧空间区域范围内存在竖直向上、场强大小E1=0.2N/C的匀强电场和方向垂直纸面向里磁感应强度为B=0.2T的匀强磁场。(g=10m/s2,不计一切阻力)求:
(1)解除锁定后A球获得的速度v1;
(2)碰后瞬间B球速度v2;
(3) E2大小满足什么条件时,B球能经电场E2通过MN所在的直线;(不考虑B球与地面碰撞再次弹起的情况)
(4)在满足(3)问情景下B球在电场E2中与MN的最大距离。
【答案】(1)3m/s,方向水平向右;(2)2m/s,方向水平向右;(3)E2≥0.283V/m;(4)0.142m
【解析】
(1)球和弹簧系统机械能守恒
![]()
得
![]()
即解除锁定后获得的速度大小为3m/s,方向水平向右
(2)A、B在MN处理碰撞动量守恒,系统机械能守恒
![]()
![]()
![]()
方向水平向右
(3)B球进入MN右侧后,电场力
![]() =
=![]()
即重力电场力平衡,因此小球在洛伦兹力作用下做匀速圆周运动,由牛顿第二定律得
![]()
在电磁场区域运动半个圆周后速度方向垂直MN水平向左射出,出射点距M点距离
![]()
在MN左侧的运动竖直方向为自由落体运动,水平方向类似于竖直上抛运动,若B球返回MN,必须满足(向右为正方向):
![]()
![]()
得
![]()
(4)由以上可知当![]() (
(![]() )时,B球恰好能回到M点,在此过程中水平方向速度为零时距离MN最远
)时,B球恰好能回到M点,在此过程中水平方向速度为零时距离MN最远
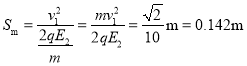

练习册系列答案
相关题目