题目内容
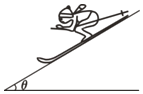
【题目】一名滑雪者乘坐缆车沿索道到达滑道顶部,索道长为x=600m,缆车速度大小恒为v车=1.2m/s;然后从滑道顶部由静止沿滑道直线滑下,滑道倾角θ=30°(简化模型如图).假设滑雪者速度vt≤10m/s时阻力可忽略,vt>10m/s时阻力为滑雪者重力的0.1倍,取g=10m/s2,求:
(1)滑雪者乘坐缆车沿索道运动到滑道顶部需要的时间;
(2)滑雪者速度v=5m/s时,加速度的大小和方向;
(3)滑雪者从滑道顶部向下滑行l=22m需要的时间
【答案】(1)500s;(2)5m/s2,方向沿滑道向下;(3)3s。
【解析】
(1)根据匀速运动的位移和速度求出滑雪者乘坐缆车沿索道运动到滑道顶部需要的时间;
(2)根据牛顿第二定律求出滑雪者的加速度大小和方向。
(3)根据速度时间公式求出速度达到10m/s的时间,以及结合位移公式求出速度达到10m/s时的位移,根据牛顿第二定律求出有摩擦时的加速度,结合位移时间公式求出继续匀加速运动的时间,从而得出总时间。
(1)滑雪者乘坐缆车时,根据x=v车t0得,![]() 。
。
(2)当滑雪者的速度v=5m/s,加速度大小为a1,mgsinθ=ma1,
解得a1=gsinθ=10×![]() m/s2=5m/s2,方向沿滑道向下。
m/s2=5m/s2,方向沿滑道向下。
(3)当滑雪者速度达到10m/s时,用时为t1,
则![]() ,
,
位移x1=![]() a1t12=
a1t12=![]() ×5×4m=10m,
×5×4m=10m,
滑雪者还要沿直线向下滑行x2=l-x1=22-10m=12m,
根据牛顿第二定律得,mgsinθ-0.1mg=ma2,
代入数据解得a2=4m/s2,
根据x2=vtt2+![]() a2t22得,代入数据解得t2=1s。
a2t22得,代入数据解得t2=1s。
共用时t=t1+t2=2s+1s=3s。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目