题目内容
 如图所示,两个小球固定在一根长为L的杆的两端,绕杆上的O点做圆周运动.当小球A的速度为vA时,小球B的速度为vB,则轴心O到小球A的距离是( )
如图所示,两个小球固定在一根长为L的杆的两端,绕杆上的O点做圆周运动.当小球A的速度为vA时,小球B的速度为vB,则轴心O到小球A的距离是( )分析:本题主要考察了物体做圆周运动时线速度、角速度、半径等物理量之间的关系,在本题中注意两球做圆周运动时角速度相等这一隐含条件.
解答:解:设球A的半径为rA,球B的半径为rB,则有rA+rB=L,
vA+vB=ωrA+ωrB=ωL ①
vA=ωrA ②
rA=
,由此可知选项ACD错误,B正确.
故选B.
vA+vB=ωrA+ωrB=ωL ①
vA=ωrA ②
rA=
| vAL |
| vA+vB |
故选B.
点评:本题通过噶“杆”模型考察了线速度、角速度、半径等物理量之间的关系,题意新颖,有思维含量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
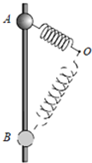 如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连,小球在A处时弹簧处于压缩状态.现将小球从A点由静止释放,沿竖直杆运动到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹力大小相等.在小球由A到B的过程中( )
如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连,小球在A处时弹簧处于压缩状态.现将小球从A点由静止释放,沿竖直杆运动到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹力大小相等.在小球由A到B的过程中( )| A、加速度大小等于重力加速度g的位置有两个 | B、小球运动到与O点等高的位置时,弹簧弹力的功率不为零 | C、弹簧弹力对小球先做正功再做负功 | D、小球到达B点时的速度一定为零 |
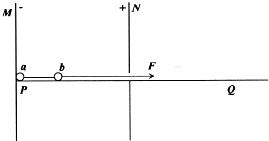 如图所示,MN是两块竖直放置的带电平行板,板内有水平向左的匀强电场,PQ是光滑绝缘的水平滑槽,滑槽从N板中间穿入电场.a、b为两个带等量正电荷的相同小球,两球之间用绝缘水平轻杆固连,轻杆长为两板间距的
如图所示,MN是两块竖直放置的带电平行板,板内有水平向左的匀强电场,PQ是光滑绝缘的水平滑槽,滑槽从N板中间穿入电场.a、b为两个带等量正电荷的相同小球,两球之间用绝缘水平轻杆固连,轻杆长为两板间距的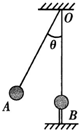 如图所示,用等长的绝缘线分别悬挂两个质量、电荷量都相同的带电小球A和B,两线上端固定于O点,B球固定在O点正下方.当A球静止时,两悬线夹角为θ.能保持夹角θ不变的方法是( )
如图所示,用等长的绝缘线分别悬挂两个质量、电荷量都相同的带电小球A和B,两线上端固定于O点,B球固定在O点正下方.当A球静止时,两悬线夹角为θ.能保持夹角θ不变的方法是( )
