题目内容
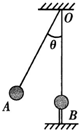如图所示，用等长的绝缘线分别悬挂两个质量、电荷量都相同的带电小球A和B，两线上端固定于O点，B球固定在O点正下方．当A球静止时，两悬线夹角为θ．能保持夹角θ不变的方法是（ ）分析：小球A受力平衡，受重力、静电斥力和拉力，三力平衡，结合平衡条件分析即可．
解答：解：小球A受力平衡，受重力、静电斥力和拉力，三力平衡，重力和静电斥力的合力沿着绳子伸长的方向，只要重力和静电斥力的合力方向不变，球就能保持平衡；
A、同时使两悬线长度减半，若角度θ不变，球间距减半，根据公式F=k
，静电斥力增加为4倍，故重力和静电斥力的合力方向一定改变，不能在原位置平衡，故A错误；
B、同时使A球的质量和电荷量减半，A球的重力和静电力都减小为一半，故重力和静电斥力的合力方向不变，球能保持平衡，故B正确；
C、同时使两球的质量和电荷量减半，A球的重力减小为一半，静电力都减小为四分之一，故故重力和静电斥力的合力方向一定改变，不能在原位置平衡，故C错误；
D、同时使两悬线长度和两球的电荷量减半，球间距减为一半，根据公式F=k
，静电力不变，故重力和静电斥力的合力方向不变，球能保持平衡，故D正确；
故选BD．
A、同时使两悬线长度减半，若角度θ不变，球间距减半，根据公式F=k
| r2 |
B、同时使A球的质量和电荷量减半，A球的重力和静电力都减小为一半，故重力和静电斥力的合力方向不变，球能保持平衡，故B正确；
C、同时使两球的质量和电荷量减半，A球的重力减小为一半，静电力都减小为四分之一，故故重力和静电斥力的合力方向一定改变，不能在原位置平衡，故C错误；
D、同时使两悬线长度和两球的电荷量减半，球间距减为一半，根据公式F=k
| r2 |
故选BD．
点评：本题关键是明确小球间静电力和重力的合力方向不变时，球就能在原位置保持平衡，不难．
练习册系列答案
阅读快车系列答案
相关题目
。在此截面所在的平面内，一条光线以45°的入射角从AC边的中点M射入棱镜。画出光路图，并求光线从棱镜射出的点的位置(不考虑光线沿原路返回的情况)。
计算出加速度．发现绝大多数情况下，根据公式计算出的加速度要比利用纸带测出的加速度大．若该同学实验操作过程没有错误，试分析其原因．（至少写两点）________________________________
计算出加速度．发现绝大多数情况下，根据公式计算出的加速度要比利用纸带测出的加速度大．若该同学实验操作过程没有错误，试分析其原因．（至少写两点）________________________________
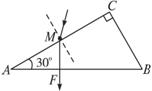
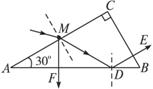
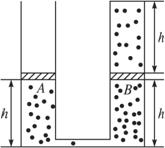
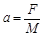计算出加速度．发现绝大多数情况下，根据公式计算出的加速度要比利用纸带测出的加速度大．若该同学实验操作过程没有错误，试分析其原因．（至少写两点）________________________________
两点的相对距离不变，相对运动轨迹为圆弧，VA=VB+VAB,在AB连线上
）
、 x=
）
为多少时，司机都是看见冰雹都是以竖直方向从车的正面玻璃上弹开？（冰雹相对地面是竖直下落的）
大小相同。
+ u2 － 2v合ucos120°
后消参数θ。
，可知B端相对A的转动线速度为：v转 + vAsinθ= 
。
= v相 
+ 
= 1 ，为椭圆；（2）vPx = avActgθ ，vPy =（1 － a）vA