题目内容
11. 如图所示,原长分别为L1和L2、劲度系数分别为k1和k2的轻质弹簧竖直悬挂在天花板上.两弹簧之间有一质量为m1的物体,最下端挂着质量为m2的另一物体,整个装置处于静止状态.
如图所示,原长分别为L1和L2、劲度系数分别为k1和k2的轻质弹簧竖直悬挂在天花板上.两弹簧之间有一质量为m1的物体,最下端挂着质量为m2的另一物体,整个装置处于静止状态.(1)这时两个弹簧的总长度为多大?
(2)若用一个质量为M的平板把下面的物体竖直缓慢地向上托起,直到两个弹簧的总长度等于两弹簧的原长之和,求这时平板受到上面物体m2的压力.
分析 (1)分别对两个弹簧运用胡克定律列式求解伸长量,然后求和;
(2)分别对两物体进行分析,根据平衡关系可求得形变量及压力大小.
解答 解:(1)劲度系数为k1轻质弹簧受到的向下拉力(m1+m2)g,设它的伸长量为x1,根据胡克定律有:
(m1+m2)g=k1 x1
解得:${x_1}=\frac{{({m_1}+{m_2})g}}{k_1}$
劲度系数为k2轻质弹簧受到的向下拉力m2g,设它的伸长量为x2,根据胡克定律有:
m2g=k2 x2
解得:${x_2}=\frac{{{m_2}g}}{k_2}$
这时两个弹簧的总长度为:L=L1+L2+x1+x2=L1+L2+$\frac{{({m_1}+{m_2})g}}{k_1}$+$\frac{{{m_2}g}}{k_2}$
(2)用一个平板把下面的物体竖直缓慢地向上托起,直到两个弹簧的总长度等于两弹簧的原长之和时,下面的弹簧应被压缩x,上面的弹簧被拉伸x.
以m1为对象,根据平衡关系有
(k1+k2)x=m1g
解得:$x=\frac{{{m_1}g}}{{{k_1}+{k_2}}}$
以m2为对象,设平板对m2的支持力为FN,根据平衡关系有
FN=k2x+m2g=k2×$\frac{{{m_1}g}}{{{k_1}+{k_2}}}$+m2g=$\frac{{{k_2}{m_1}g}}{{{k_1}+{k_2}}}$+m2g=$\frac{{{k_1}{m_2}g+{k_2}({m_1}+{m_2})g}}{{{k_1}+{k_2}}}$
故这时平板受到下面物体m2的压力FN'=$\frac{{{k_1}{m_2}g+{k_2}({m_1}+{m_2})g}}{{{k_1}+{k_2}}}$.
答:(1)这时两个弹簧的总长度为L1+L2+$\frac{{({m_1}+{m_2})g}}{k_1}$+$\frac{{{m_2}g}}{k_2}$;
(2)这时平板受到上面物体m2的压力为$\frac{{{k_1}{m_2}g+{k_2}({m_1}+{m_2})g}}{{{k_1}+{k_2}}}$
点评 求出本题的关键注意研究对象的选择;同时知道当两个弹簧的总长度等于两弹簧原长之和时,上边弹簧的伸长量与下边弹簧的压缩量相等.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
| A. | 1Ω | B. | 2Ω | C. | 3Ω | D. | 4Ω |
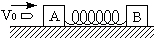 如图所示,A、B两个木块用弹簧相连接,它们静止在光滑的水平面上,A和B的质量分别为9m和20m.一颗质量为m的子弹以速度V0水平射入木块内没有穿出,在后来的过程中弹簧的弹性势能的最大值等于多大?
如图所示,A、B两个木块用弹簧相连接,它们静止在光滑的水平面上,A和B的质量分别为9m和20m.一颗质量为m的子弹以速度V0水平射入木块内没有穿出,在后来的过程中弹簧的弹性势能的最大值等于多大? 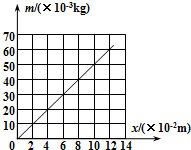 某同学探究弹力与弹簧伸长量的关系.弹簧自然悬挂,长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如表:
某同学探究弹力与弹簧伸长量的关系.弹簧自然悬挂,长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如表:| 代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
| 数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.4 | 35.35 | 37.40 | 39.30 |
(2)如图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与Lx的差值(填“L0或Lx”).
(3)由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g(结果均保留两位有效数字,g取9.8m/s2).
| A. | 线圈平面每经过中性面一次,感应电流方向就改变一次,感应电动势方向不变 | |
| B. | 线圈转动一周,感应电流的方向一定改变一次 | |
| C. | 线圈平面每经过中性面一次,感应电流和感应电动势方向都改变一次 | |
| D. | 线圈转动一周,感应电流和感应电动势方向一定都改变一次 |
 用油膜法估测分子直径
用油膜法估测分子直径 某实验小组为了体验伽利略理想实验的魅力,利用一块长方形的薄钢片放在两个等高的支架上,做成一个底部凹形由光滑弧面连接的双斜面.该装置可以简化为如图所示模型,斜面与水平面的夹角为θ.现保持小滑块在左侧斜面上的初始释放高度H不变,每次都将小滑块由静止释放.小滑块和斜面间的动摩擦因数为μ.
某实验小组为了体验伽利略理想实验的魅力,利用一块长方形的薄钢片放在两个等高的支架上,做成一个底部凹形由光滑弧面连接的双斜面.该装置可以简化为如图所示模型,斜面与水平面的夹角为θ.现保持小滑块在左侧斜面上的初始释放高度H不变,每次都将小滑块由静止释放.小滑块和斜面间的动摩擦因数为μ. 如图所示,质量为m的物体用细绳OC悬挂在支架上的O点,轻杆OB的B端由铰链固定,可绕B点自由转动,细绳OA与轻杆OB所成的角为θ,求细绳OA中张力T的大小和轻杆OB所受弹力FN的大小?
如图所示,质量为m的物体用细绳OC悬挂在支架上的O点,轻杆OB的B端由铰链固定,可绕B点自由转动,细绳OA与轻杆OB所成的角为θ,求细绳OA中张力T的大小和轻杆OB所受弹力FN的大小?