��Ŀ����
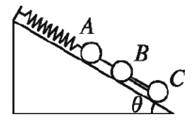
����Ŀ����ͼ��ʾ��ˮƽľ����㹻����ˮƽ���ʹ�ƽ���Խӣ�����Ϊ2kg��С����A��ֹ��ľ���ϣ�����ҲΪ2kg��С���B��ֹ��ľ�����ˣ��������ʹ��Ҷ˴������A�����ʱ������һˮƽ����ij���I=8Ns���ã��˶�l=3m�������B�����������������B�������ϴ��ʹ������ʹ�ʼ����v=1m/s���ٶ�˳ʱ��ת��������һ��ʱ�����B�����A�ٴη�����ײ������ͣ��ľ�����ˣ���֪���A��ľ�塢���B���ʹ�֮��Ķ�Ħ��������=0.2��ȡg=10m/s2 �� 
��1�������A�����B��һ����ײǰ˲���ٶȵĴ�С��
��2�����B�봫�ʹ��Ħ�����������ܣ�
��3�����A��ľ���Ħ�����������ܣ�
���𰸡�
��1���⣺�ɶ��������ã�I=mv0
�� v0=4m/s
�ɶ��ܶ����é���mgl= ![]() ��
�� ![]()
��ã����A�����B��һ����ײǰ˲���ٶȴ�С v1=2m/s
�����A�����B��һ����ײǰ˲���ٶȵĴ�С��2m/s��
��2�����һ����ײ��˲������A��B���ٶȴ�С�ֱ�Ϊv1�䡢v2��ȡ����Ϊ�������ݶ����غ㶨�ɵã�
mv1=mv1��+mv2��
�ɶ����غ�ã�
![]() mv12=
mv12= ![]() mv1��2+
mv1��2+ ![]() mv22��
mv22��
��� v1��=0��v2=2m/s����֪��ײ���������彻���ٶȣ�
���B�ڴ��ʹ��˶��ļ��ٶȴ�СΪ a= ![]() =��g=2m/s2��
=��g=2m/s2��
���B�����ٶȼ�Ϊ0ʱ�˶��ľ�����Ϊx1����
v22=2ax1��
��� x1=1m
�ٶȱ�Ϊ0���õ�ʱ�� t1= ![]() =
= ![]() =1s
=1s
���ʹ��˶��ľ��� x2=vt1=1��1m=1m
�ù�����Ħ������������ Q1=��mg��x1+x2��
��� Q1=8J
���B���Ҽ����ٶȱ�Ϊ1m/sʱ�˶��ľ�����Ϊx3����
v2=2ax3��
��� x3=0.25m
���õ�ʱ�� t2= ![]() =
= ![]() =0.5s
=0.5s
�ù����д��ʹ��˶��ľ��� x4=vt2=1��0.5m=0.5m
�ù�����Ħ������������ Q2=��mg��x4��x3��
��� Q2=1J
�����B�봫�ʹ��Ħ������������Ϊ Q=Q1+Q2=9J
�����B�봫�ʹ��Ħ��������������9J��
��3�����Ϸ���֪��B��A�ٴ���ײ���������彻���ٶȣ���ײ˲��A���ٶ� v3=v=1m/s
�ʸ��ݹ��ܹ�ϵ�ɵã�
���A��ľ���Ħ������������ QA=��mgl+ ![]()
��� QA=13J
�����A��ľ���Ħ��������������13J��
����������1��������������̷dz����ӡ���Ҫ�ȴӷ���������˶��������֡��ж��������Ͷ��ܶ���������ʽ��⡣
��2���������һ����ײ�������㶯���غ㣬���ݶ����غ������ײ����ٶȣ����B���ϴ��ʹ����˶����̷ֳ�����������Ħ������������������Ħ�����������λ����ʽ��⡣
��3��Ħ������������������Ħ�����������λ�ơ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�