题目内容
【题目】如图所示,一根轻质弹簧一端固定在天花板的木桩上,另一端连接一个质量为m的小球,最初弹簧处于水平且为原长,现将小球由静止释放,当小球第一次运动到最低点时弹簧刚好竖直,此时弹簧的弹性势能为Ep , 弹簧的长度为l,弹簧的弹力大小为F,小球的加速度大小为a,重力加速度为g,则( )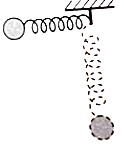
A.F= ![]()
B.F= ![]()
C.a= ![]()
D.a= ![]()
【答案】B,C
【解析】解:设小球运动到最低点时的速度大小为v.
根据小球和弹簧组成的系统机械能守恒得:
mgl=Ep+ ![]()
在最低点,由向心力公式得:F﹣mg=m ![]() =ma
=ma
联立解得 F= ![]() ,a=
,a= ![]() .
.
故选:BC
【考点精析】关于本题考查的向心力和机械能守恒及其条件,需要了解向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力;在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变才能得出正确答案.

练习册系列答案
相关题目
【题目】下表是按照密立根的方法进行光电效应实验时得到的某金属的遏止电压Uc和入射光的频率v的几组数据.
U0/V | 0.541 | 0.637 | 0.714 | 0.809 | 0.878 |
V/1014Hz | 5.644 | 5.888 | 6.098 | 6.303 | 6.501 |
由以上数据应用Execl描点连线,可得直线方程,如图所示.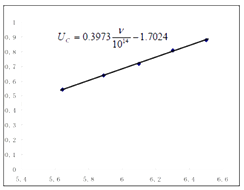
则这种金属的截止频率约为( )
A.3.5×1014Hz
B.4.3×1014Hz
C.5.5×1014Hz
D.6.0×1014Hz