题目内容
5.某同学利用图甲所示的实验装置,验证动能定理:
(1)在用质量为m钩码的重力表示小车所受合外力的条件下,在图乙中1、3两点间对质量为M的小车用实验验证动能定理的表达式为$\frac{M}{8{t}^{2}}$[(x3+x4)2-(x1+x2)2].(用题和图中所涉及数据的字母表示,两个计数点间的时间间隔用t表示)
(2)实验时为了保证滑块受到的合力与沙桶的总重力大小基本相等,沙和沙桶的总质量应满足的条件是B,实验时首先要做的步骤是D.(以上两空填字母代表)
A.避免小车在运动过程中发生抖动
B.沙和沙桶的总质量远小于滑块的质量
C.将木板不带滑轮的一端适当垫高,使小车在钩码拉动下恰好做匀速运动
D.将木板不带滑轮的一端适当垫高,在不挂钩码的情况下使小车恰好做匀速运动.
分析 (1)根据功的计算公式求得钩码重力做功,动能的变化量等于1、3两点的动能之差;
(2)实验要测量滑块动能的增加量和合力做的功,用沙和沙桶的总质量表示滑块受到的拉力,对滑块受力分析,受到重力、拉力、支持力和摩擦力,要使拉力等于合力,必须使重力的下滑分量等于摩擦力;同时重物加速下降,处于失重状态,故拉力小于重力,可以根据牛顿第二定律列式求出拉力表达式分析讨论;
解答 解:(1)重力势能的减小量为:△EP=mg(x2+x3);
而v1=$\frac{{x}_{1}+{x}_{2}}{2T}$;
同理,v3=$\frac{{x}_{3}+{x}_{4}}{2T}$;
那么动能的增加量为:△Ek=$\frac{1}{2}m({v}_{3}^{2}-{v}_{1}^{2})$=$\frac{M}{8{t}^{2}}$[(x3+x4)2-(x1+x2)2].
因此1、3两点间对小车用实验验证动能定理的表达式为:mg(x2+x3)=$\frac{M}{8{t}^{2}}$[(x3+x4)2-(x1+x2)2].
(2)沙和沙桶加速下滑,处于失重状态,其对细线的拉力小于重力,设拉力为T,根据牛顿第二定律,
对沙和沙桶,有 mg-T=ma
对滑块,有 T=Ma
解得:
T=$\frac{M}{M+m}$
故当M>>m时,有T≈mg
滑块下滑时受到重力、细线的拉力、支持力和摩擦力,要使拉力等于合力,则应该用重力的下滑分量来平衡摩擦力,故可以将长木板的一段垫高;故选:BD;
故答案为:(1)$\frac{M}{8{t}^{2}}$[(x3+x4)2-(x1+x2)2].(2)B;D.
点评 本题关键是根据实验原理并结合牛顿第二定律和动能定理来确定要测量的量、实验的具体操作方法和实验误差的减小方法.

练习册系列答案
相关题目
20.物体以速度v0水平抛出,若不计空气阻力,则当其竖直方向的位移与水平方向的位移相等时,以下说法中不正确的是( )
| A. | 竖直分速度为$\sqrt{2}$v0 | B. | 即时速度大小为$\sqrt{5}$v0 | ||
| C. | 运动的时间为$\frac{2{v}_{0}}{g}$ | D. | 运动的位移为$\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$ |
10.物理学研究表明,自然界存在四种基本相互作用.关于重力、弹力、摩擦力,下列说法正确的是( )
| A. | 都属于万有引力相互作用 | |
| B. | 重力和弹力属于万有引力相互作用,摩擦力属于弱相互作用 | |
| C. | 重力属于万有引力相互作用,弹力属于强相互作用,摩擦力属于弱相互作用 | |
| D. | 重力属于万有引力相互作用,弹力和摩擦力属于电磁相互作用 |
17.一列简谐横波,在t=5.0s时的波形如图甲所示,图乙是这列波中质点P的振动图线,那么该波的传播速度和传播方向是( )


| A. | v=0.25 m/s,向右传播 | B. | v=0.50 m/s,向右传播 | ||
| C. | v=0.25 m/s,向左传播 | D. | v=0.50 m/s,向左传播 |
19. 在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,电表示数变化量的绝对值分别用△I、△U1、△U2和△U3如表示,下列式子正确的是( )
在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,电表示数变化量的绝对值分别用△I、△U1、△U2和△U3如表示,下列式子正确的是( )
 在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,电表示数变化量的绝对值分别用△I、△U1、△U2和△U3如表示,下列式子正确的是( )
在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,电表示数变化量的绝对值分别用△I、△U1、△U2和△U3如表示,下列式子正确的是( )| A. | $\frac{U_1}{I}>\frac{{△{U_1}}}{△I}$ | B. | $\frac{U_2}{I}>\frac{{△{U_2}}}{△I}$ | C. | |△U1|+|△U2|=|△U3| | D. | |△U1|+|△U3|=|△U2| |
 如图,A、B、C、D四个物块重均为100N,作用在B的水平力F=20N,A、B、C三个物体放在桌面上,物块D用两轻绳吊在A和天花板上,两轻绳与水平面的夹角均为45°,整个系统静止,求A和B之间的摩擦力.
如图,A、B、C、D四个物块重均为100N,作用在B的水平力F=20N,A、B、C三个物体放在桌面上,物块D用两轻绳吊在A和天花板上,两轻绳与水平面的夹角均为45°,整个系统静止,求A和B之间的摩擦力.


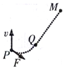
 一人骑摩托车追赶距他h=400m处的平直公路上正以v0=54km/h的速度匀速行驶的一辆汽车,当摩托车与汽车相距d=500m时,此人开始沿一条直线匀速追赶汽车,如图所示.问此人应以多大的最小速度向什么方向运动才能追上目标?这种情况下对应的时间为多少?
一人骑摩托车追赶距他h=400m处的平直公路上正以v0=54km/h的速度匀速行驶的一辆汽车,当摩托车与汽车相距d=500m时,此人开始沿一条直线匀速追赶汽车,如图所示.问此人应以多大的最小速度向什么方向运动才能追上目标?这种情况下对应的时间为多少? 某电视台娱乐节目,要求选手要从较高的平台上以水平速度v0跃出后,落在水平传送带上,已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20.85m,由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,经过一个△t=0.5s反应时间后,立刻以a=2m/s2,方向向右的加速度跑至传送带最右端.
某电视台娱乐节目,要求选手要从较高的平台上以水平速度v0跃出后,落在水平传送带上,已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20.85m,由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,经过一个△t=0.5s反应时间后,立刻以a=2m/s2,方向向右的加速度跑至传送带最右端.