题目内容
14. 某电视台娱乐节目,要求选手要从较高的平台上以水平速度v0跃出后,落在水平传送带上,已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20.85m,由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,经过一个△t=0.5s反应时间后,立刻以a=2m/s2,方向向右的加速度跑至传送带最右端.
某电视台娱乐节目,要求选手要从较高的平台上以水平速度v0跃出后,落在水平传送带上,已知平台与传送带高度差H=1.8m,水池宽度S0=1.2m,传送带AB间的距离L0=20.85m,由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,经过一个△t=0.5s反应时间后,立刻以a=2m/s2,方向向右的加速度跑至传送带最右端.(1)若传送带静止,选手以v0=3m/s水平速度从平台跃出,求从开始跃出到跑至传送带右端经历的时间.
(2)若传送带以u=1m/s的恒定速度向左运动,选手若要能到达传送带右端,则从高台上跃出的水平速度V1至少多大?(3)在第(2)问的条件下,如果选手以v1的最小速度跃出,求从开始跃出到跑至传送带右端经历的时间.
分析 (1)根据高度求出平抛运动的时间,根据水平位移求出在传送带上做匀加速运动的位移,结合位移时间公式求出匀加速运动的时间,再结合反应时间求出总时间.
(2)根据速度位移公式求出向左做匀减速运动的位移和匀速运动的位移,从而得出平抛运动的最小水平位移,根据平抛运动的时间求出平抛运动的最小初速度.
(3)根据匀减速运动的时间和反向做匀加速运动的时间,结合平抛运动的时间和反应时间求出总时间.
解答 解:(1)根据H=$\frac{1}{2}g{{t}_{1}}^{2}$得,平抛运动的时间${t}_{1}=\sqrt{\frac{2H}{g}}=\sqrt{\frac{2×1.8}{10}}s=0.6s$,
水平位移x1=v0t1=3×0.6m=1.8m,
在传送带上匀加速直线运动的位移x2=L0-(x1-s0)=20.85-0.6m=20.25m,
根据${x}_{2}=\frac{1}{2}a{{t}_{2}}^{2}$得,${t}_{2}=\sqrt{\frac{2×20.25}{2}}s=4.5s$,
则t=t1+t2+△t=0.6+4.5+0.5s=5.6s.
(2)选手落在传送带上在反应时间内向左的位移x3=u△t=1×0.5m=0.5m,
向左做匀减速直线运动的位移${x}_{4}=\frac{{u}^{2}}{2a}=\frac{1}{2×2}m=0.25m$,
则平抛运动的最小水平位移x′=x3+x4+s0=0.5+0.25+1.2m=1.95m,
则平抛运动的最小速度${v}_{1}=\frac{x′}{{t}_{1}}=\frac{1.95}{0.6}m/s=3.25m/s$.
(3)向左匀减速运动的时间${t}_{3}=\frac{u}{a}=\frac{1}{2}s=0.5s$,
返回做匀加速运动的时间${t}_{4}=\sqrt{\frac{2{L}_{0}}{a}}=\sqrt{\frac{2×20.85}{2}}s≈4.57s$,
从开始跃出到跑至传送带右端经历的时间t′=t1+△t+t3+t4=0.6+0.5+0.5+4.57s=6.17s.
答:(1)从开始跃出到跑至传送带右端经历的时间为5.6s;
(2)从高台上跃出的水平速度V1至少为3.25m/s;
(3)从开始跃出到跑至传送带右端经历的时间为6.17s.
点评 解决本题的关键分析出选手的运动情况,然后根据平抛运动和运动学公式求解.

| A. | 人造卫星b的周期较大 | B. | 人造卫星b的线速度较大 | ||
| C. | 人造卫星b的角速度较大 | D. | 人造卫星b的向心加速度较大 |
 如图所示,质量为m的汽车在平直公路上行驶,所受的阻力恒为车重的k倍.汽车以额定功率行驶,当它加速行驶的速度为v时,加速度为a.则以下分析正确的是( )
如图所示,质量为m的汽车在平直公路上行驶,所受的阻力恒为车重的k倍.汽车以额定功率行驶,当它加速行驶的速度为v时,加速度为a.则以下分析正确的是( )| A. | 汽车发动机的额定功率为kmgv | |
| B. | 汽车行驶的最大速度为$\frac{(kg+a)v}{kg}$ | |
| C. | 当汽车加速度减小到$\frac{a}{2}$时.速度增加到2v | |
| D. | 汽车发动机的额定功率为mav |
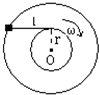 如图所示,手持一根长为L的轻绳的一端在水平桌面上做半径为r、角速度为ω的匀速圆周运动,绳始终保持与该圆周相切,绳的另一端系一质量为m的小木块,木块也在桌面上做匀速圆周运动,则( )
如图所示,手持一根长为L的轻绳的一端在水平桌面上做半径为r、角速度为ω的匀速圆周运动,绳始终保持与该圆周相切,绳的另一端系一质量为m的小木块,木块也在桌面上做匀速圆周运动,则( )| A. | 绳对木块不做功 | |
| B. | 绳的拉力大小为$m{ω^2}\sqrt{{l^2}+{r^2}}$ | |
| C. | 绳拉木块做功的功率等于$\frac{{m{ω^3}r({l^2}+{r^2})}}{l}$ | |
| D. | 木块受重力、桌面的支持力和绳子的拉力作用 |
 如图所示,ⅠⅡ分别是甲,乙两小球从同一地点沿同一直线运动的V-t图线,根据图线可以判断( )
如图所示,ⅠⅡ分别是甲,乙两小球从同一地点沿同一直线运动的V-t图线,根据图线可以判断( )| A. | 甲、乙两小球做的是初速度方向相反的匀减速直线运动,加速度大小相同,方向相同 | |
| B. | 两球在t=4s时相距最远 | |
| C. | 两球在t=2s时刻速度相同 | |
| D. | 两球在t=8s时相遇 |
| A. | 小孔成像的原理利用了光的衍射现象 | |
| B. | 光导纤维传输信号是利用了光的全反射现象 | |
| C. | 用分光镜观测光谱是利用了光折射时的色散现象 | |
| D. | 用标准平面检查光学平面的平整程度是利用了光的偏振现象 | |
| E. | 在阳光照射下,水面的油膜上出现彩色花纹是光的干涉现象 |

 如图为中国”玉免号”月球车在月球水平面运动时的场景.假设月球车质量为m,在月球车电板充满电的情况下,月球车在月球水平面上从静止出发沿同-方向做直线运动的最大行驶距离为L,月球车运动时受到的阻力为车重的k倍.已知月球表面重力加速度为地球的六分之一,地球表面的重力加速度为go,求:
如图为中国”玉免号”月球车在月球水平面运动时的场景.假设月球车质量为m,在月球车电板充满电的情况下,月球车在月球水平面上从静止出发沿同-方向做直线运动的最大行驶距离为L,月球车运动时受到的阻力为车重的k倍.已知月球表面重力加速度为地球的六分之一,地球表面的重力加速度为go,求: