Question

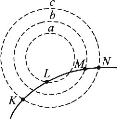
【题目】如图所示，在水平的桌面上，有一光滑的弧形轨道，其底端恰好与光滑水平面相切。右侧有一竖直放置的光滑圆弧轨道MNP，轨道半径R＝0.8m，MN为其竖直直径，P点到桌面的竖直距离也是R，质量为M＝2.0kg的小物块B静止在水平面上。质量为mA＝2.0kg的小物块A从距离水平面某一高度h的S点沿轨道从静止开始下滑，经过弧形轨道的最低点Q滑上水平面与B发生弹性碰撞，碰后两个物体交换速度，然后小物块B从桌面右边缘D点飞离桌面后，恰由P点沿圆轨道切线落入圆轨道，g＝10m/s2，则

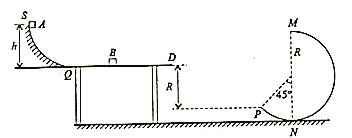
A.物块B离开D点时的速度大小为4m/s

B.物块B落到P点时其竖直速度大于物块B离开D点时的速度

C.S与Q竖直高度为0.8m

D.物块能沿轨道到达M点的速度大小约为2.2m/s

Answer 1

【答案】AC

【解析】

AB.A、B碰撞后，因二者交换速度，所以A静止，物块B由D点以初速度vD做平抛运动，落到P点时其竖直速度为vy，有vy2＝2gR，而

＝tan45°

解得vD＝vy＝4m/s,选项A正确、B错误；

C.设A与B碰撞前的速度为，A与B相碰交换速度，所以v0=vD＝4m/s,A从S滑到Q的过程中，根据机械能守恒定律得

mAgh＝mAv02

解得h＝0.8m,选项C正确；

D.设物块能沿轨道到达M点，且到达时其速度为vM，从D到M由动能定理得：

－mBgRcos45°＝mBvM2－mBvD2，

解得

vM≈2.2m/s<≈2.8m/

即物块不能到达M点，选项D错误。