��Ŀ����
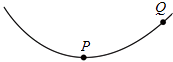
����Ŀ������������Ŀ��ظ�ʹ�õ����ػ����ӡ�ȳ�������ƿ��ظ�ʹ�õ�����ɴ���Ԥ�ƽ���2030�귢��ɹ����������ʹӡ����̫������ռ�����ơ�����ij�ɴ��ذ뾶ΪR��Բ���Ƶ������У���Բ����ΪT������뾶ΪR0.�÷ɴ�Ҫ���ص���ʱ�����ڹ����ij��A�������ʽ����ʵ���ֵ���Ӷ������Ե���Ϊ�������Բ����˶�����Բ���������B�����У���ͼ��ʾ����÷ɴ���A���˶���B�������ʱ�䡣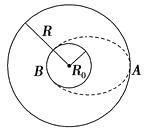
���𰸡��⣺�ɴ��ذ뾶ΪR��Բ���Ƶ����˶�ʱ������Ϊ��볤��a��R
�ɴ����ص���ʱ�����Ե���Ϊ�������Բ������У��ɴ���A���˶���B���ʱ��Ϊ������Բ����˶�����T���һ�롣
��Բ����İ볤��a�䣽 ![]() ��R��R0��
��R��R0��
�ɿ����յ������ɵ� ![]()
����t�� ![]() T�䣽
T�䣽 ![]()
![]()
��������������Ҫ���鿪���յ������ɵ������Ӧ�ã����������Ҫ����������ͬ����µİ볤������ڣ��ɴ˽������̽�����⣬�ɴ�����ߵ㽵�䵽��������ʱ��ֻ�а�����ڡ�

��ϰ��ϵ�д�
�����Ŀ