题目内容
9.①在利用重物自由下落“验证机械能守恒定律”的实验中,打点计时器所用电源频率为f=50Hz,实验要求打点计时器在打第一个点时释放纸带.甲、乙、丙三个学生分别用同一装置各打出一条纸带,量出各纸带上第1、2两点间的距离分别为0.48cm,0.19cm和0.18cm,肯定其中一个学生在操作上有错误,该同学是甲.其错误的操作是先释放重物后接通电源.
②丁同学用甲图所示装置进行实验,得到如图乙所示的纸带,把第一个点(初速度为零)记作O点,测出O、A间的距离为68.97cm,点A、C间的距离为15.24cm,点C、E间的距离16.76cm,已知当地重力加速度为g=9.8m/s2,重锤的质量为m=1.0kg则打点计时器在打O点到C点的这段时间内,重锤动能的增加量为8.00J,重力势能的减少量为8.25J.(保留三位有效数字)
③利用这个装置也可以测量重锤下落的加速度=9.50m/s2(结果保留三位有效数字)
④在实验中发现,重锤减小的重力势能总大于重锤最大的动能,其原因主要是因为在重锤带着纸带下落过程中存在着阻力的作用,用题目给出的已知量.求出重锤下落过程中受到的平均阻力大小为0.30N.
⑤若利用BD段来验证机械能守恒,则还要测量的物理量是BD段的长度,要验证的表达式是$\frac{1}{2}$m($\frac{{x}_{CE}}{2}$f)2-$\frac{1}{2}$m($\frac{{x}_{AC}}{2}$f)2(用题中符号表达)
⑥以下是几位同学的操作步骤,其中有错误和不必要的有ACDG
A.用天平测量重锤的质量m
B.按如图装置把打点计时器安装在铁架台上,用导线把打点计时器与学生电源的交流电压输出档连接好.
C.把纸带的一端在重锤上用夹子固定好,另一端穿过计时器限位孔,竖直提起纸带使重锤停靠距打点计时器较远的地方,纸带上端用夹子夹住.
D.松开纸带,接通电源,让重锤自由下落.
E.重复几次,得到3~5条打好点的纸带.
F.在打好点的纸带中挑选第一、二两点间的距离接近2mm,且点迹清晰的一条纸带,在起始点标上0,以后各计时点依次标上1,2,3…,用刻度尺测出对应下落高度h1、h2、h3….
G.应用公式vn=ghn计算各点对应的即时速度v1、v2、v3….
H.计算各点对应的势能减少量mghn和动能的增加量$\frac{1}{2}$mvn2,进行比较.再做出结论.
分析 ①做自由下落物体在0.02s内下落的高度大约2mm,从而确定甲在操作上错误.1、2两个点的距离偏大,可知初速度不为零,操作的错误在于先释放重物后接通电源.
②根据某段时间内的平均速度等于中间时刻的瞬时速度求出C点的瞬时速度,从而得出C点的动能,知道重锤动能的增加量.根据重力做功求出重力势能的减小量.
③根据连续相等时间内的位移之差是一恒量,即△x=aT2求出重锤下落的加速度.
④重锤受重力和阻力,根据牛顿第二定律列式求解.
⑤利用BD段来验证机械能守恒,则还要测量的物理量是BD长度,再根据重物在这两段的平均速度来表示其瞬时速度,从而可知物体减小的重力势能与滑块及物体增加的动能关系,进而得以验证;
⑥解决实验问题首先要掌握该实验原理,了解实验的仪器、操作步骤和数据处理以及注意事项.
解答 解:①若物体做自由下落,在0.02s内的位移大约在2mm左右,可见甲同学的操作错误,使得重物的初速度不为零,即先释放重物后接通电源.
②C点的速度等于AE段的平均速度:vC=$\frac{0.1524+0.1676}{4×0.02}$m/s=4m/s,
则动能的增加量:△Ek=$\frac{1}{2}$mvC2=$\frac{1}{2}$×1×16J=8.00J
重力势能的减小量:△Ep=mgh=9.8×(68.97+15.24)×10-2=8.25J.
③根据△x=aT2得:a=$\frac{△x}{{T}^{2}}$=$\frac{0.1676-0.1524}{0.0{4}^{2}}$m/s2=9.50m/s2.
④重锤减小的重力势能总大于重锤增加的动能,其原因主要是因为在重锤带着纸带下落过程中存在着阻力的作用;
根据牛顿第二定律,有:mg-f=ma
解得:f=m(g-a)=1×(9.8-9.5)=0.3N;
⑤利用BD段来验证机械能守恒,则还要测量的物理量是BD长度,从而可求出从B到D的减小的重力势能;
再由某段平均速度等于其中时刻的瞬时速度,则有:△EK=$\frac{1}{2}$m($\frac{{x}_{CE}}{2}$f)2-$\frac{1}{2}$m($\frac{{x}_{AC}}{2}$f)2
因此,验证的表达式是:mgxBD=$\frac{1}{2}$m($\frac{{x}_{CE}}{2}$f)2-$\frac{1}{2}$m($\frac{{x}_{AC}}{2}$f)2;
⑥不必要的步骤是:A、因为我们是比较mgh、$\frac{1}{2}$mv2的大小关系,故m可约去比较,不需要用天平.故A错误.
有错误或不妥的步骤是:B、固定好打点计时器,将连着重锤的纸带穿过限位孔,用手提住,让纸带下端尽量靠近打点计时器,以便测出更多的数据,以减小误差.故B错误.
D、接通电源,松开纸带,让重锤自由下落.故D错误;
G、不能运用此公式vn=ghn计算各点对应的即时速度,否则起不到实验验证,而是理论推导,故G错误;
故选:ACDG.
故答案为:①甲,先释放重物后接通电源;
②8.00;8.25;
③9.50;
④因为在重锤带着纸带下落过程中存在着阻力的作用;0.30;
⑤BD段的长度,$\frac{1}{2}$m($\frac{{x}_{CE}}{2}$f)2-$\frac{1}{2}$m($\frac{{x}_{AC}}{2}$f)2
⑥ACDG.
点评 利用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用,提高解决问题能力.要注意单位的换算和有效数字的保留.
本题借助于光电门来算瞬时速度,并将物体与滑块作为一整体来研究,注意在实验过程中要尽量减小系统受到的阻力.

 快捷英语周周练系列答案
快捷英语周周练系列答案 如图所示,在一个等边三角形ABC的两个顶点B、C处各放一个点电荷,测得A处的电场强度大小为E,方向与BC边平行,拿走C处的点电荷后,A处电场强度将是( )
如图所示,在一个等边三角形ABC的两个顶点B、C处各放一个点电荷,测得A处的电场强度大小为E,方向与BC边平行,拿走C处的点电荷后,A处电场强度将是( )| A. | 大小仍为E,方向从A指向B | B. | 大小仍为E,方向从B指向A | ||
| C. | 大小变为$\frac{E}{2}$,方向不变 | D. | 大小变为$\frac{E}{2}$,方向从B指向A |
| A. | 质量越大的质点,水平位移越大 | |
| B. | 质量越小的质点,水平位移越大 | |
| C. | 初速度越大的质点,空中运动时间越长 | |
| D. | 初速度越大的质点,落地速度越大 |
 如图所示,在半径为R的圆内,有方向为垂直纸面向里的匀强磁场,一带电粒子以速度v沿半径aO方向从a点射入磁场,又从c点射出磁场,射出时速度方向偏转60°,则粒子在磁场中运动的时间是( )
如图所示,在半径为R的圆内,有方向为垂直纸面向里的匀强磁场,一带电粒子以速度v沿半径aO方向从a点射入磁场,又从c点射出磁场,射出时速度方向偏转60°,则粒子在磁场中运动的时间是( )| A. | $\frac{πR}{3v}$ | B. | $\frac{\sqrt{3}πR}{3v}$ | C. | $\frac{2πR}{3v}$ | D. | $\frac{2\sqrt{3}πR}{3v}$ |
| A. | 物体一定处于静止状态 | |
| B. | 物体一定处于匀速直线运动状态 | |
| C. | 若物体处于静止状态,则F1、F3的合力大小一定为28N,方向指向正南 | |
| D. | 若物体处于匀加速直线运动状态,则最大加速度为9m/s2,方向指向正北 |
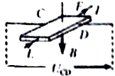 利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域,如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作而向下,通入图示方向的电流I,C、D两侧面会形成电势差UCD,下列说法中正确的是( )
利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域,如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作而向下,通入图示方向的电流I,C、D两侧面会形成电势差UCD,下列说法中正确的是( )| A. | 电势差UCD与村料有关 | |
| B. | 若霍尔元件的载流子是自由电子,则电势差UCD>0 | |
| C. | 仅增大磁感应强度时,电势差UCD不变 | |
| D. | 在测定地球赤道上方的地磁场强弱时,元件的工作面应保持竖直 |
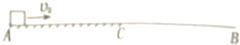 如图所示,在冰面上将一滑块从A点以初速度v0推出,滑块与冰面的动摩擦因数为μ,滑块到达B点时速度为$\frac{3}{4}$v0.
如图所示,在冰面上将一滑块从A点以初速度v0推出,滑块与冰面的动摩擦因数为μ,滑块到达B点时速度为$\frac{3}{4}$v0.