��Ŀ����
����Ŀ����ͼ��ʾ,���Ϊ�ȵ�б����PP�䡢QQ��֮��ֲڣ��ҳ�Ϊ3L�����ಿ�ֶ��⻬����״��ͬ�������ֲ����ȵ����鱡ľ��A��B�� C��б��������һ�𣬵���ճ�ӡ�ÿ�鱡ľ�峤��ΪL��������Ϊm����б��PP�䡢QQ���Ķ�Ħ��������Ϊ3tan�ȡ������Ǵ�PP���Ϸ�ij���ɾ�ֹ�ͷţ����鱡ľ�����ͨ��QQ�䡣�������ٶ�Ϊg����
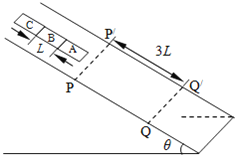
(1)��ľ��A�¶��˶�����QQ��֮ǰ�ٶ�����λ�ã�
(2)��ľ��B�϶˵���PP��ʱ�ܵ�ľ��C�����Ĵ�С��
(3)�Է����ͷ�A��B��Cʱ����ľ��A�¶���PP���������ʲô����������ʹ���鱡ľ�����ͨ��QQ�䡣
���𰸡�(1)L (2)2mgsin�� (3)![]()
��������
��1����ľ��A��PP�䡢QQ����˶�ʱ�������鱡ľ�忴�����壬�������»����»�������Ħ����ʱ�˶��ٶȴ����ֵ���ɴ���ʽ��⻬��A���¶���P���ľ�����
��2����������ľ������������ţ�ٵڶ������������ļ��ٶȣ��ٸ���C����ţ�ٵڶ�������B��C����������
��3��Ҫʹ������ľ�嶼�ܻ���QQ�䴦����ľ��C��![]() ��QQ�䴦ʱ�����ٶ�Ӧ����������ľ��Cȫ��Խ��PP��ǰ����ľ�������ѹ�ţ�ȫ����PP�䡢QQ��֮���˶�������������뿪QQ��ʱ����ľ���������ġ��ֶ��ɶ��ܶ�����ʽ�����
��QQ�䴦ʱ�����ٶ�Ӧ����������ľ��Cȫ��Խ��PP��ǰ����ľ�������ѹ�ţ�ȫ����PP�䡢QQ��֮���˶�������������뿪QQ��ʱ����ľ���������ġ��ֶ��ɶ��ܶ�����ʽ�����
(1)��ľ��A��PP�䡢QQ����˶�ʱ�������鱡ľ�忴�����塣�������»���������б���������Ħ����ʱ���˶��ٶȴ����ֵ���У�![]() ���ã�
���ã�![]()
������A���¶���P��Lʱ���ٶ����
(2)����ľ��B���϶˵���PP��ʱ����������ľ��������ţ�ٵڶ������У�
![]() ���ã�
���ã�![]()
��C��ľ����ţ�ٵڶ������У�![]() ��
��
�ã�![]() ��������б�����ϣ�����ţ�ٵ������ɿ�֪����ľ��B�϶˵���PP��ʱ�ܵ�ľ��C�����Ĵ�СΪ
��������б�����ϣ�����ţ�ٵ������ɿ�֪����ľ��B�϶˵���PP��ʱ�ܵ�ľ��C�����Ĵ�СΪ![]() ��������б�����¡�
��������б�����¡�
(3)Ҫʹ������ľ�嶼�ܻ���QQ�䴦����ľ��C��![]() ��QQ�䴦ʱ�����ٶ�Ӧ�����㡣
��QQ�䴦ʱ�����ٶ�Ӧ�����㡣
��ľ��Cȫ��Խ��PP��ǰ����ľ�����ѹ�ţ���ľ��ȫ����PP�䡢QQ��֮���˶�ʱ������������뿪QQ��ʱ����ľ���������ġ�
��Cľ��պ�ȫ��Խ��PP��ʱ�ٶ�Ϊv.
��ľ��C�Ӹպ�Խ��PP�䵽ľ��C��![]() ����QQ�䴦�ٶ�Ϊ0���ö��ܶ����У�
����QQ�䴦�ٶ�Ϊ0���ö��ܶ����У�
![]() ��
��![]()
�迪ʼ�»�ʱ��A���¶���PP�䴦����Ϊx������ľ��Ӹ��ͷŵ�ľ��C�Ӹպ�Խ��PP�������ö��ܶ����У�![]()
�õ���![]()
����ʹ���鱡ľ�����ͨ��QQ����ͷ�λ����ľ��A�¶���PP�����x���㣺![]() ��
��