Question

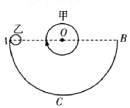
【题目】在倾角为θ的光滑斜面上有两个用轻弹簧连接的物块A和B，它们的质量分别为m和3m，弹簧的劲度系数为k，C为一固定挡板，系统处于静止状态。现用一沿斜面向上的拉力拉物块A，使之沿斜面向上运动。当B即将离开C时，A的速度为v，加速度大小为a，方向沿斜面向上。求：

(1)从静止状态到B刚要离开C时，物块A上滑的位移S；

(2)从静止状态到B刚要离开C时，弹簧增加的弹性势能

Answer 1

【答案】(1) (2)

【解析】未加拉力F时，物体A对弹簧的压力等于其重力的下滑分力，由胡克定律求得弹簧的压缩量；物块B刚要离开C时，弹簧的拉力等于物体B重力的下滑分力，根据平衡条件并结合胡克定律求出弹簧的伸长量，从而求出A发生的位移；由功能关系可得弹簧弹性势能的增加量等于拉力的功减去系统动能和重力势能的增加量。

(1)开始时，设弹管压缩量为，则根据平衡等式有：

当B即将要离开C时，设弹簧伸长量为，则有

所以A发生的位移为

(2)对A受力分析，当B即将离开C时，已知A此时加速度为a，

根据牛顿第二定律有

得

对系统，根据能量守恒：当物块B刚离开C时，弹簧弹性势能增加量为：

代入得