题目内容
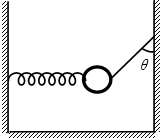
如图所示,质量为m的小球与轻弹簧和轻绳相连处于静止,弹簧处于水平状态,劲度系数为k;轻绳与竖直墙壁的夹角θ=45°,重力加速度为g.
(1)求弹簧的伸长量△x;
(2)现烧断轻绳,求轻绳烧断瞬间小球的加速度.
(1)求弹簧的伸长量△x;
(2)现烧断轻绳,求轻绳烧断瞬间小球的加速度.

(1)对小球受力分析如图所示,由平衡条件有:
弹簧弹力F=mgtanθ①
又由胡克定律有:F=k△x②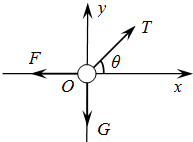
由①②式可得:△x=
(2)烧断瞬间,设小球加速度为a,此时F、G不变,
小球合力F合=
③
又由牛顿第二定律可知F合=ma④
由③④式并代入题中数据可得:
a=
g
答:(1)弹簧的伸长量△x=
(2)轻绳烧断瞬间小球的加速度a=
g.
弹簧弹力F=mgtanθ①
又由胡克定律有:F=k△x②

由①②式可得:△x=
| mg |
| k |
(2)烧断瞬间,设小球加速度为a,此时F、G不变,
小球合力F合=
| F2+G2 |
又由牛顿第二定律可知F合=ma④
由③④式并代入题中数据可得:
a=
| 2 |
答:(1)弹簧的伸长量△x=
| mg |
| k |
(2)轻绳烧断瞬间小球的加速度a=
| 2 |

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目