题目内容
13.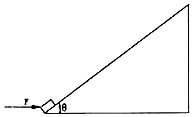 如图所示,水平恒力F=40N作用于一质量m=1kg的小物块上,使小物块由静止开始从倾角θ=37°的固定斜面底端沿斜面上滑,当小物块滑至斜面中点时,撤去F,物块恰好能滑到斜面顶端.(小物块大小可忽略,g=10m/s2,sin37°=0.6,cos37°=0.8),求小物块与斜面间的动摩擦因数μ.
如图所示,水平恒力F=40N作用于一质量m=1kg的小物块上,使小物块由静止开始从倾角θ=37°的固定斜面底端沿斜面上滑,当小物块滑至斜面中点时,撤去F,物块恰好能滑到斜面顶端.(小物块大小可忽略,g=10m/s2,sin37°=0.6,cos37°=0.8),求小物块与斜面间的动摩擦因数μ.
分析 根据匀变速直线运动速度位移公式求出水平恒力F作用时和撤去时的加速度关系,然后对小物块受力分析,
水平恒力F作用时和撤去时,分别根据牛顿第二定律列方程联立即可求出小物块与斜面间的动摩擦因数μ.
解答 解:设斜面的长度为L,小物块滑至斜面中点时的速度为v,
由速度位移公式得,v2-0=2a1•$\frac{L}{2}$---①
撤去F,由速度位移公式得,0-v2=-2a2•$\frac{L}{2}$---②
联立①②可解得:a1=a2,---③
对小物块受力分析,沿斜面方向上,
由牛顿第二定律得,Fcosθ-mgsinθ-μ(mgcosθ+Fsinθ)=ma1---④
撤去F,由牛顿第二定律得,mgsinθ+μmgcosθ=ma2---⑤
联立③④⑤代入数据可解得:μ=0.5.
答:小物块与斜面间的动摩擦因数μ为0.5.
点评 本题主要考查了牛顿第二定律和运动学基本公式的直接应用,解题的关键是正确对物体进行受力分析,难度不大.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
4.一条河宽为d,河水流速为v1,小船在静水中的速度为v2,要使小船在渡河过程中所行路程S最短,则( )
| A. | 当v1>v2时,s=$\frac{\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{{v}_{1}}$d | B. | 当v1<v2时,s=$\frac{\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{{v}_{1}}$d | ||
| C. | 当v1>v2时,s=$\frac{{v}_{1}}{{v}_{2}}$d | D. | 当v2<v1,s=$\frac{{v}_{2}}{{v}_{1}}$d |
1.如图所示,某健身爱好者手拉着轻绳,在粗糙的水平地面上缓慢地移动,保持绳索始终平行于地面.为了锻炼自己的臂力和腿部力量,可以在O点悬挂不同的重物C.则( )

| A. | 若健身者缓慢向右移动,绳OA拉力变小 | |
| B. | 若健身者缓慢向左移动,绳OB拉力变大 | |
| C. | 著健身者缓慢向右移动,绳OA、OB拉力的合力变大 | |
| D. | 若健身者缓慢向左移动,健身者与地面间的摩擦力变小 |
8. 如图所示为由二极管构成的逻辑电路,A、B为输入端,Y为输出端,高电位用真值“1”表示,低电位用真值“0”表示,则( )
如图所示为由二极管构成的逻辑电路,A、B为输入端,Y为输出端,高电位用真值“1”表示,低电位用真值“0”表示,则( )
 如图所示为由二极管构成的逻辑电路,A、B为输入端,Y为输出端,高电位用真值“1”表示,低电位用真值“0”表示,则( )
如图所示为由二极管构成的逻辑电路,A、B为输入端,Y为输出端,高电位用真值“1”表示,低电位用真值“0”表示,则( )| A. | A=0,B=0时Y=0 | B. | A=1,B=0时Y=1 | C. | A=0,B=1时Y=1 | D. | A=1,B=1时Y=1 |
5.图关于一些现象和技术的应用,表述正确的是( )

| A. | 甲图用传感器观察震荡电流:回路电阻和向外辐射电磁波造成震荡电路能量的减小 | |
| B. | 乙图CT检查病人身体:CT是利用β射线照射人体 | |
| C. | 丙图检查平面表面平整度图样:利用光的干涉原理 | |
| D. | 丁图用激光打孔:利用激光具有高度相干性特点 |
2.以某一水平初速度抛出一石块,不计空气阻力,下列对石块在运动过程中的说法,正确的是( )
| A. | 在两个下落高度相同的过程中,石块受到的冲量相同 | |
| B. | 在两个相等的时间间隔内,石块受到的冲量相同 | |
| C. | 在两个下落高度相同的过程中,石块动量的增量相同 | |
| D. | 在两个相等的时间间隔内,石块动量的増量相同 |
8.一石块做自由落体运动,到达地面.把它在空中运动的时间分为相等的三段,如果它在第一段时间内的位移是2m,那么它在第三段时间内的位移是( )
| A. | 4.0 m | B. | 6.0m | C. | 8.0 m | D. | 10.0 m |

 等腰三棱镜ABC顶角为120°,AB边长度为16cm,一束单色光平行于底边BC从AB边上的O1点射入三棱镜,在BC边发生全反射后从AC边的O1点射出三棱镜,射到屏上的D点,其中O1、O、O2三点均为对应边的中点,光在真空中的传播速度为3×108m/s.
等腰三棱镜ABC顶角为120°,AB边长度为16cm,一束单色光平行于底边BC从AB边上的O1点射入三棱镜,在BC边发生全反射后从AC边的O1点射出三棱镜,射到屏上的D点,其中O1、O、O2三点均为对应边的中点,光在真空中的传播速度为3×108m/s.