题目内容
3.某科学家提出年轻热星体中核聚变的一种理论,其中的两个核反应方程为:①${\;}_1^1$H+${\;}_6^{12}$C→${\;}_7^{13}$N②${\;}_1^1$H+${\;}_7^{15}$N-→${\;}_6^{12}$C+X
(1)写出原子核X的元素符号、质量数和核电荷数;
(2)已知原子核${\;}_1^1$H、${\;}_6^{12}$C、${\;}_7^{13}$N的质量分别为mH=1.0078u、mC=12.0000u、mN=13.0057u,1u相当于931MeV.试求每发生一次上述聚变反应①所释放的核能;(结果保留三位有效数字)
(3)用上述辐射中产生的波长为λ=4×10-7m的单色光去照射逸出功为W=3.0×10-19J金属材料铯时,通过计算判断能否产生光电效应?若能,试求出产生的光电子的最大初动能.(普朗克常量h=6.63×10-34J•s,光在空气中的速度c=3×108m/s)(结果保留三位有效数字)
分析 (1)根据质量数与质子数守恒规律,即可求解;
(2)根据爱因斯坦质能方程,结合质量亏损求出释放的核能;
(3)根据光电效应的条件判断能否发生光电效应,通过光电效应方程求出光电子的最大初动能.
解答 解:(1)根据质量数与质子数守恒规律,${\;}_1^1$H+${\;}_7^{15}$N-→${\;}_6^{12}$C+${\;}_{2}^{4}$He;
(2)根据爱因斯坦质能方程得,△E=(mH+mC-mN)×931=1.9551 MeV
(3)单色光的能量为E=h$\frac{c}{λ}$=6.63×10-34×$\frac{3×1{0}^{8}}{4×1{0}^{-7}}$=4.97×10-19J>3.0×10-19J
所以可以产生光电效应.
最大初动能为Ekm=hv-W0=4.9725×10-19-3.0×10-19=1.97×10-19J.
答:(1)原子核X的元素${\;}_2^4$He;
(2)每发生一次上述聚变反应①所释放的核能1.9551 MeV;
(3)可以产生光电效应,产生的光电子的最大初动能1.97×10-19J.
点评 解决本题的关键掌握光电效应方程和爱因斯坦质能方程,并能灵活运用.

练习册系列答案
相关题目
16. 如图所示为一简谐横波在某一时刻的波形图.已知图中质点F此时刻的运动向是竖直向下的,(即负Y轴方向)那么( )
如图所示为一简谐横波在某一时刻的波形图.已知图中质点F此时刻的运动向是竖直向下的,(即负Y轴方向)那么( )
 如图所示为一简谐横波在某一时刻的波形图.已知图中质点F此时刻的运动向是竖直向下的,(即负Y轴方向)那么( )
如图所示为一简谐横波在某一时刻的波形图.已知图中质点F此时刻的运动向是竖直向下的,(即负Y轴方向)那么( )| A. | 这列波正在向右传播(即正X轴方向) | |
| B. | 此时刻质点H与F的运动方向相同 | |
| C. | 从此时刻起,质点E的运动方向是正Y轴方向 | |
| D. | 从此时刻起,质点C将比B点先回到平衡位置 |
14.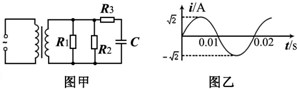 如图甲所示,理想变压器原线圈通有正弦式交变电流,副线圈接有3个电阻和一个电容器.已知R1=R3=20Ω,R2=40Ω,原、副线圈的匝数比为10:1,原线圈的输入功率为P=35W,已知通过R1的正弦交流电如图乙所示,则R2的电功率及流过电容器C的电流分别为( )
如图甲所示,理想变压器原线圈通有正弦式交变电流,副线圈接有3个电阻和一个电容器.已知R1=R3=20Ω,R2=40Ω,原、副线圈的匝数比为10:1,原线圈的输入功率为P=35W,已知通过R1的正弦交流电如图乙所示,则R2的电功率及流过电容器C的电流分别为( )
 如图甲所示,理想变压器原线圈通有正弦式交变电流,副线圈接有3个电阻和一个电容器.已知R1=R3=20Ω,R2=40Ω,原、副线圈的匝数比为10:1,原线圈的输入功率为P=35W,已知通过R1的正弦交流电如图乙所示,则R2的电功率及流过电容器C的电流分别为( )
如图甲所示,理想变压器原线圈通有正弦式交变电流,副线圈接有3个电阻和一个电容器.已知R1=R3=20Ω,R2=40Ω,原、副线圈的匝数比为10:1,原线圈的输入功率为P=35W,已知通过R1的正弦交流电如图乙所示,则R2的电功率及流过电容器C的电流分别为( )| A. | 20W 1.75A | B. | 20W 0.25A | C. | 10W 0.25A | D. | 10W 0.50A |
11. 粗细均匀、全长为L米的链条,对称地挂在轻小而光滑的定滑轮上如图.轻轻拉动一下链条的一端,使它从静止开始运动,则链条脱离滑轮的瞬间,其速度的大小为( )
粗细均匀、全长为L米的链条,对称地挂在轻小而光滑的定滑轮上如图.轻轻拉动一下链条的一端,使它从静止开始运动,则链条脱离滑轮的瞬间,其速度的大小为( )
 粗细均匀、全长为L米的链条,对称地挂在轻小而光滑的定滑轮上如图.轻轻拉动一下链条的一端,使它从静止开始运动,则链条脱离滑轮的瞬间,其速度的大小为( )
粗细均匀、全长为L米的链条,对称地挂在轻小而光滑的定滑轮上如图.轻轻拉动一下链条的一端,使它从静止开始运动,则链条脱离滑轮的瞬间,其速度的大小为( )| A. | $\sqrt{gL}$ | B. | $\frac{1}{2}\sqrt{gL}$ | C. | $\sqrt{2gL}$ | D. | $\frac{1}{2}\sqrt{2gL}$ |
18. 如图所示,足够长的固定光滑斜面倾角为θ,质量为m的物体以速度υ从斜面底端冲上斜面,达到最高点后又滑回原处,所用时间为t.对于这一过程,下列判断正确的是( )
如图所示,足够长的固定光滑斜面倾角为θ,质量为m的物体以速度υ从斜面底端冲上斜面,达到最高点后又滑回原处,所用时间为t.对于这一过程,下列判断正确的是( )
 如图所示,足够长的固定光滑斜面倾角为θ,质量为m的物体以速度υ从斜面底端冲上斜面,达到最高点后又滑回原处,所用时间为t.对于这一过程,下列判断正确的是( )
如图所示,足够长的固定光滑斜面倾角为θ,质量为m的物体以速度υ从斜面底端冲上斜面,达到最高点后又滑回原处,所用时间为t.对于这一过程,下列判断正确的是( )| A. | 斜面对物体的弹力的冲量为零 | B. | 物体受到的合力的冲量大小为零 | ||
| C. | 物体受到的重力的冲量大小为mgt | D. | 物体动量的变化量大小为mgtsinθ |
8.以一定的初速度竖直上抛一小球,上升的最大高度为h,小球的质量为m,运动中所受空气的阻力大小恒为f,则从抛出至回到抛出点的过程中,重力和空气阻力对小球做的功分别为( )
| A. | 0,-2fh | B. | 2mgh,0 | C. | 2mgh,2fh | D. | 0,0 |

 一物体从离地面5m处竖直抛出,上升10m后最终落到地面上,以抛出点为原点,向上为正方向,建立坐标系(如图),则上升阶段的位移为10m,下降阶段的位移为-15m,全过程的位移是-5m,全过程的路程是25m.
一物体从离地面5m处竖直抛出,上升10m后最终落到地面上,以抛出点为原点,向上为正方向,建立坐标系(如图),则上升阶段的位移为10m,下降阶段的位移为-15m,全过程的位移是-5m,全过程的路程是25m.