题目内容
10.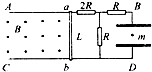 如图所示,在竖直平面内有足够长的两平行金属导轨AB、CD.导轨间距为L,电阻不计.一根电阻不计的金属棒ab可在导轨上无摩擦地滑动.棒与导轨垂直,并接触良好.导轨之间有垂直纸面向外的匀强磁场,磁感强度为B.导轨右边与电路连接.电路中的三个定值电阻阻值分别为2R、R和R.在BD间接有一水平放置的电容为C的平行板电容器,板间距离为d.当ab以速度v0匀速向左运动时,电容器中质量为m的带电微粒恰好静止于两极板中间位置.( )
如图所示,在竖直平面内有足够长的两平行金属导轨AB、CD.导轨间距为L,电阻不计.一根电阻不计的金属棒ab可在导轨上无摩擦地滑动.棒与导轨垂直,并接触良好.导轨之间有垂直纸面向外的匀强磁场,磁感强度为B.导轨右边与电路连接.电路中的三个定值电阻阻值分别为2R、R和R.在BD间接有一水平放置的电容为C的平行板电容器,板间距离为d.当ab以速度v0匀速向左运动时,电容器中质量为m的带电微粒恰好静止于两极板中间位置.( )| A. | 微粒带负电 | |
| B. | 电容器的带电量为$\frac{CBL{v}_{0}}{2}$ | |
| C. | 若ab棒以速度2v0向左运动,微粒将经过时间$\sqrt{\frac{d}{g}}$到达上极板 | |
| D. | 若ab棒在外力作用下由静止开始在导轨上作简谐运动,运动中的最大速度为v0,则流经2R的最大电流为$\frac{BL{v}_{0}}{3R}$ |
分析 当ab以速度v0匀速向左运动时,产生感应电动势,根据右手定则可知感应电流方向,确定出电容器两极板的电性.根据微粒受力平衡即可判断微粒的电性,由平衡条件可求出电量的大小.若ab棒以速度2v0向左运动,电容器板间电压增大,根据牛顿第二定律求出加速度,由位移公式求解微粒到达上极板所用时间.根据法拉第电磁感应定律和欧姆定律求最大电流.
解答 解:A、ab棒匀速向左运动时,棒中产生的感应电流方向为b→a,则电容器上板带正电,下板带负电,板间场强方向向下.
微粒受力平衡,电场力方向向上,则微粒带负电,故A正确.
B、电容器板间电压 UC=$\frac{1}{3}$E=$\frac{1}{3}$BLv0,电容器的带电量为Q=CUC=$\frac{1}{3}$CBLv0,故B错误.
C、当ab以速度v0匀速向左运动时,由微粒平衡,有 mg=q$\frac{{U}_{C}}{d}$
若ab棒以速度2v0向左运动,由上知,板间电压为2UC,根据牛顿第二定律得 q$\frac{2{U}_{C}}{d}$-mg=ma,可得 a=g
根据$\frac{1}{2}$d=$\frac{1}{2}a{t}^{2}$,得 t=$\sqrt{\frac{d}{a}}$=$\sqrt{\frac{d}{g}}$,即微粒将经过时间$\sqrt{\frac{d}{g}}$到达上极板.故C正确.
D、若ab棒在外力作用下由静止开始在导轨上作简谐运动,运动中的最大速度为v0,则棒产生的最大感应电动势为 Em=BLv0
由于电容器“通交流”,则有电流流过与电容器串联的电阻R,所以流经2R的最大电流为Im≠$\frac{BL{v}_{0}}{3R}$.故D错误.
故选:AC
点评 本题是电容器、电路、电磁感应、力学等知识的综合,只要掌握基本知识就能正确解答.要掌握电容器“通交流,隔直流”的特性.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | 电磁炉 | B. | 微波炉 | C. | 金属探测器 | D. | 真空冶炼炉 |
| A. | 爱因斯坦光电效应方程是:$\frac{1}{2}$mvm2=hν-W | |
| B. | 只要光照射的时间足够长,任何金属都能产生光电效应 | |
| C. | 无论光强多强,只要光的频率小于金属的极限频率就不能产生光电效应 | |
| D. | 发生光电效应时,入射光频率越大所产生的光电子的最大初动能就越大 |
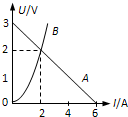 如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡的U-I图线,用该电源和小灯泡组成闭合电路时,电源的输出功率和电源的总功率分别是( )
如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡的U-I图线,用该电源和小灯泡组成闭合电路时,电源的输出功率和电源的总功率分别是( )| A. | 4 W,8 W | B. | 4W,6 W | C. | 2 W,3 W | D. | 2 W,4 W |
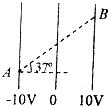 如图所示,某匀强电场中三个等势面及其对应的电势值,若A、B两点间的距离是2.5cm,则该匀强电场的场强大小为多少?
如图所示,某匀强电场中三个等势面及其对应的电势值,若A、B两点间的距离是2.5cm,则该匀强电场的场强大小为多少?