题目内容
如图所示,小车的质量为M=3kg,车的上表面左端为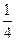 光滑圆弧BC,右端为水平粗糙平面AB,二者相切于B点,AB的长为
光滑圆弧BC,右端为水平粗糙平面AB,二者相切于B点,AB的长为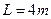 ,一质量为
,一质量为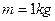 的小物块,放在车的最右端,小物块与车之间的动摩擦因数
的小物块,放在车的最右端,小物块与车之间的动摩擦因数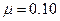 。车和小物块一起以
。车和小物块一起以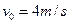 的速度在光滑水平面上匀速向左运动,小车撞墙后瞬间速度变为零,但未与墙粘连。g取
的速度在光滑水平面上匀速向左运动,小车撞墙后瞬间速度变为零,但未与墙粘连。g取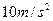 ,求:
,求:
(1)小物块沿圆弧上升的最大高度;
(2)小物块再次回到B点时的速度大小;
(3)小物块从最高点返回后与车的速度相同时,小物块距B端多远。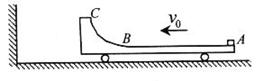
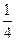 光滑圆弧BC,右端为水平粗糙平面AB,二者相切于B点,AB的长为
光滑圆弧BC,右端为水平粗糙平面AB,二者相切于B点,AB的长为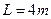 ,一质量为
,一质量为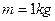 的小物块,放在车的最右端,小物块与车之间的动摩擦因数
的小物块,放在车的最右端,小物块与车之间的动摩擦因数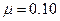 。车和小物块一起以
。车和小物块一起以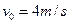 的速度在光滑水平面上匀速向左运动,小车撞墙后瞬间速度变为零,但未与墙粘连。g取
的速度在光滑水平面上匀速向左运动,小车撞墙后瞬间速度变为零,但未与墙粘连。g取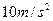 ,求:
,求:(1)小物块沿圆弧上升的最大高度;
(2)小物块再次回到B点时的速度大小;
(3)小物块从最高点返回后与车的速度相同时,小物块距B端多远。

(1)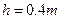 (2)
(2)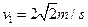 (3)小物块停在距离B点3m的位置上
(3)小物块停在距离B点3m的位置上
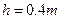 (2)
(2)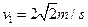 (3)小物块停在距离B点3m的位置上
(3)小物块停在距离B点3m的位置上(1)对小物块从开始到上升到最高点的过程用能量守恒得

代入已知条件得
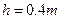
(2)对小物块从开始到返回到B点的过程用动能定理得
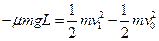
代入已知得
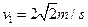
(3)小物块从B点向右滑行过程中,小物块与车组成的系统动量守恒
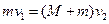
代入已知条件得
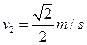
小物块相对车向右滑行的过程中,对系统用能量守恒得
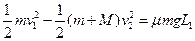
由④⑤⑥⑦并代入已知条件得
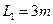
即小物块停在距离B点3m的位置上。

代入已知条件得
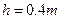
(2)对小物块从开始到返回到B点的过程用动能定理得
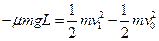
代入已知得
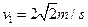
(3)小物块从B点向右滑行过程中,小物块与车组成的系统动量守恒
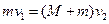
代入已知条件得
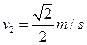
小物块相对车向右滑行的过程中,对系统用能量守恒得
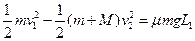
由④⑤⑥⑦并代入已知条件得
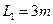
即小物块停在距离B点3m的位置上。

练习册系列答案
相关题目
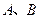 ,质量分别为
,质量分别为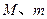 ,物块
,物块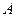 右端栓接轻弹簧1。现用物块
右端栓接轻弹簧1。现用物块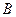 将固定在墙壁上的弹簧2缓慢压缩,当弹簧2的弹性势能为
将固定在墙壁上的弹簧2缓慢压缩,当弹簧2的弹性势能为 时,释放物块
时,释放物块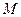 比
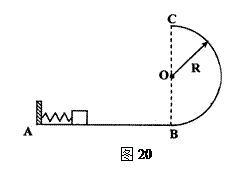
比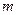 大得多,物块
大得多,物块
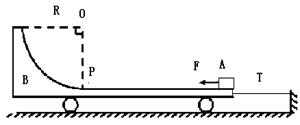 如图所示,水平光滑地面上停放着一辆小车B,其质量为M=4Kg,右端用细绳T系在墙上,小车的四分之一圆弧轨道半径为R=1.7m,在最低点P处与长为L=2m的水平轨道相切,可视为质点的质量为m=2Kg物块A放在小车B的最右端,A与B的动摩擦因数为μ=0.4,整个轨道处于同一竖直平面内。现对A施加向左的水平恒力F=48.5N,当A运动到P点时,撤去F,同时剪断细绳,物块恰好能到达圆弧的最高点,当其再次返回P点时,动能为第一次过P点时的
如图所示,水平光滑地面上停放着一辆小车B,其质量为M=4Kg,右端用细绳T系在墙上,小车的四分之一圆弧轨道半径为R=1.7m,在最低点P处与长为L=2m的水平轨道相切,可视为质点的质量为m=2Kg物块A放在小车B的最右端,A与B的动摩擦因数为μ=0.4,整个轨道处于同一竖直平面内。现对A施加向左的水平恒力F=48.5N,当A运动到P点时,撤去F,同时剪断细绳,物块恰好能到达圆弧的最高点,当其再次返回P点时,动能为第一次过P点时的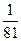 。取g=10m/s2。求
。取g=10m/s2。求 (m),匀质柔软绳长度L=3m,质量m=0.9kg,搭放在圆柱体上,绳子右端A刚好与圆心O等高。(g=10m/s2)
(m),匀质柔软绳长度L=3m,质量m=0.9kg,搭放在圆柱体上,绳子右端A刚好与圆心O等高。(g=10m/s2)
 =2m/s,同时给A端竖直向下的力F2,为保持A端在一段时间内竖直向下匀速运动,则力F2与时间t之间满足什么关系?
=2m/s,同时给A端竖直向下的力F2,为保持A端在一段时间内竖直向下匀速运动,则力F2与时间t之间满足什么关系?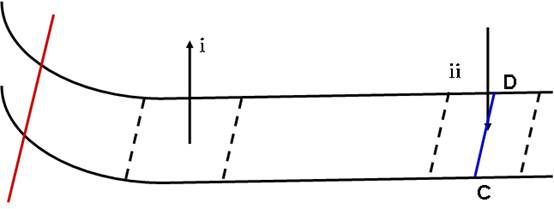
 如图所示,由电动机带动的水平传送带以速度为v=2.0 m/s匀速运行,A端上方靠近传送带料斗中装有煤,打开阀门,煤以流量为Q=50 kg/s落到传送带上,煤与传送带达共同速度后被运至B端,在运送煤的过程中,下列说法正确的是( )
如图所示,由电动机带动的水平传送带以速度为v=2.0 m/s匀速运行,A端上方靠近传送带料斗中装有煤,打开阀门,煤以流量为Q=50 kg/s落到传送带上,煤与传送带达共同速度后被运至B端,在运送煤的过程中,下列说法正确的是( )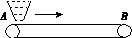
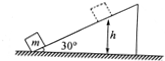
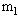 =0.2kg、
=0.2kg、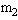 =0.6kg,用细线系住并压缩一个轻质弹簧,铁块与左侧墙的距离是8.0m(如图).现将细线烧断,小铁块在弹簧弹力作用下,沿垂直于墙的直线反向运动,铁块与水平地面间的动摩擦因数为μ=0.1.m1与墙相碰后返回追
=0.6kg,用细线系住并压缩一个轻质弹簧,铁块与左侧墙的距离是8.0m(如图).现将细线烧断,小铁块在弹簧弹力作用下,沿垂直于墙的直线反向运动,铁块与水平地面间的动摩擦因数为μ=0.1.m1与墙相碰后返回追