题目内容
【题目】如图所示，AB为倾角θ＝37°的粗糙斜面轨道，通过一小段光滑圆弧与光滑水平轨道BC相连接，质量为m2的小球乙静止在水平轨道上，质量为m1的小球甲以速度v0与乙球发生弹性正碰.若m1∶m2＝2∶3，且轨道足够长，
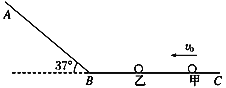
（1）第一次碰撞后的瞬间两球的速度分别多大；
（2）要使两球能发生第二次碰撞，求乙球与斜面之间的动摩擦因数μ应满足什么条件？.(sin 37°＝0.6，cos 37°＝0.8)
【答案】（1）
（2）
【解析】
解：（1）设第一次碰后甲的速度为v1，乙的速度为v2，以甲球的初速度方向为正方向，由动量守恒定律和机械能守恒定律得：
联立解得：
，负号表示方向水平向右；
（2）设上滑的最大位移大小为s，滑到斜面底端的速度大小为v，由动能定理得：
联立解得：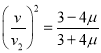
乙要能追上甲，则：
解得：
练习册系列答案
相关题目
