题目内容
【题目】如图所示,物体A、B的质量分别为m、2m,物体B置于水平面上,B物体上部半圆型槽的半径为R,将物体A从圆槽的右侧最顶端由静止释放,一切摩擦均不计。则下列选项正确的是
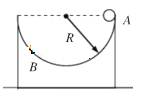
A. A不能到达B圆槽的左侧最高点
B. A运动到圆槽的最低点速度为![]()
C. B向右匀速运动
D. B向右运动的最大位移大小为![]()
【答案】D
【解析】
物体A和B组成的系统在水平方向上动量守恒,当A到达左侧的最高点时,水平方向上的速度相等,竖直方向上的速度为零,根据动量守恒定律和能量守恒定律求出A上升的最大高度以及到达最低点的速度.当A运动到左侧最高点时,B向右的位移最大,根据动量守恒定律求出最大位移的大小.
设A到达左侧最高点的速度为v,根据动量守恒定律知,由于初动量为零,则末总动量为零,即v=0,根据能量守恒定律知,A能到达B圆槽左侧的最高点。故A错误。设A到达最低点时的速度为v,根据动量守恒定律得:0=mv-2mv′,解得:v′=![]() ,根据能量守恒定律得:mgR=
,根据能量守恒定律得:mgR=![]() mv2+
mv2+![]() 2m(
2m(![]() )2,解得:
)2,解得:![]() .故B错误。因为A和B组成的系统在水平方向上动量守恒,当A在水平方向上的速度向左时,B的速度向右,当A在水平方向上的速度向右时,则B的速度向左。故C错误。因为A和B组成的系统在水平方向上动量守恒,当A运动到左侧最高点时,B向右运动的位移最大,设B向右的最大位移为x,根据动量守恒定律得:m(2R-x)=2mx,解得:x=
.故B错误。因为A和B组成的系统在水平方向上动量守恒,当A在水平方向上的速度向左时,B的速度向右,当A在水平方向上的速度向右时,则B的速度向左。故C错误。因为A和B组成的系统在水平方向上动量守恒,当A运动到左侧最高点时,B向右运动的位移最大,设B向右的最大位移为x,根据动量守恒定律得:m(2R-x)=2mx,解得:x=![]() R.故D正确。故选D。
R.故D正确。故选D。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目