题目内容
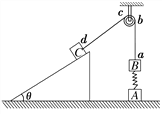
【题目】如图所示,倾角为θ的固定光滑斜面底部有一垂直斜面的固定挡板C。劲度系数为k1的轻弹簧两端分别与质量均为m的物体A和B连接,劲度系数为k2的轻弹簧一端与A连接,另一端通过细线与一轻质小桶相连,细线跨过斜面顶端的光滑的定滑轮,B靠在挡板C处,A和B均静止。现缓慢地向小桶内加入细砂,当B与挡板C恰要分离时,小桶下降的距离是多少?

【答案】
【解析】试题分析:未向小桶内加入细沙时,弹簧![]() 受到的压力大小等于A的重力沿斜面向下的分力,根据胡克定律求出此时该弹簧的压缩量.当B与挡板C间挤压力恰好为零时,弹簧
受到的压力大小等于A的重力沿斜面向下的分力,根据胡克定律求出此时该弹簧的压缩量.当B与挡板C间挤压力恰好为零时,弹簧![]() 受到的拉力等于B重力沿斜面向下的分力,弹簧
受到的拉力等于B重力沿斜面向下的分力,弹簧![]() 受到的拉力等于两个物体的总重力沿斜面向下的分力,根据胡克定律求出此时两弹簧的伸长量,再由几何关系求出小桶下降的距离.
受到的拉力等于两个物体的总重力沿斜面向下的分力,根据胡克定律求出此时两弹簧的伸长量,再由几何关系求出小桶下降的距离.
轻质小桶内未加入细砂时,弹簧![]() 处于自然长度,设此时弹簧
处于自然长度,设此时弹簧![]() 压缩量为
压缩量为![]() ,
,
对A受力分析可知: ![]()
缓慢地向小桶内加入细砂,当B与挡板C间挤压力恰好为零时,设弹簧![]() 伸长量为
伸长量为![]() ,弹簧
,弹簧![]() 伸长量为
伸长量为![]() ,
,
对B受力分析可知: ![]()
对A、B整体受力分析可知: ![]()
由分析知,小桶下降的距离: ![]() ,解得
,解得 。
。
方法二:对弹簧k1分析:初态时受到A的压力为mgsin θ,末态时对B的拉力为mgsin θ,因此弹力变化为![]() ,则由
,则由![]() 得:
得: ![]() 。
。
对弹簧![]() 分析:初态时的弹力为零,末态时产生的拉力为
分析:初态时的弹力为零,末态时产生的拉力为![]() ,则
,则![]()
所以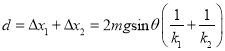 。
。

【题目】如图甲为某同学测绘额定电压为2.5V的小灯泡的I-U特性曲线的实验电路图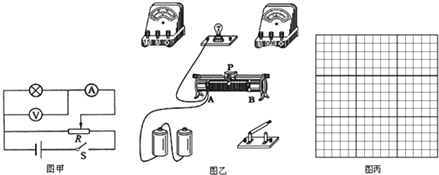
(1)根据电路图甲,用笔画线替代导线,将答题纸图乙中的实验电路图连接完整(图乙左边是电压表)
(2)依据你所连接的电路,在开关S闭合之前,滑动变阻器的滑片应该置于 ______ 端(选填“A”、“B”或“AB中间”)
(3)实验中测得有关数据如表:
U/V | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 |
I/A | 0.10 | 0.16 | 0.20 | 0.23 | 0.25 | 0.26 | 0.27 |
根据表中的实验数据,在图丙中画出小灯泡的I-U特性曲线
(4)如果用一个电动势为3V,内阻为25Ω的直流电源直接给该小灯泡供电,则小灯泡的实际功率为 ______ W.